初中数学圆幂定理解答题

按要求作图并回答：
用刻度尺作线段AC (AC＝5cm)，以A为圆心，a为半径作圆，再以C为圆心，b为半径作圆 (其中a＜5，b＜5, 且要求⊙A与⊙C交于B、D两点)，连结BD.
（1）若能作出满足要求的两圆，则a、b应满足的条件是        .
（2）求证：AC⊥BD.

《九章算术》第九章的第九题为：今有圆材，埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺．问径几何．译成现代文并配图如下：圆木埋在壁中，不知大小，用锯子来锯它，锯到深度CD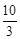＝cm时，量得锯痕AB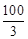＝cm，问圆木的直径是多少cm?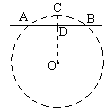

如图，AB、CD为⊙O的两条弦，AB＝CD．求证：∠AOC＝∠BOD．

如图，CD是半圆O的一条弦，CD∥AB，延长OA、OB至F、E，使，联结FC、ED，CD＝2，AB＝6。

（1）求∠F的正切值；
（2）联结DF，与半径OC交于H，求△FHO的面积。

已知在△中，∠的平分线与△的外接圆交于，过作∥.
求证：是⊙切线.

如图，△ABC内接于⊙O，且AB=AC，BD是⊙O的直径， AD与BC交于点E，F在DA的延长线上，且BF=BE．

1 23

 

（1）试判断BF与⊙O的位置关系，并说明理由；
（2）若BF=6，cosC= ，求⊙O的直径．

在Rt△ACB中，∠C=90°，AC=3cm，BC=4cm，以BC为直径作⊙O交AB于点D.

（1）求线段AD的长度；
（2）点E是线段AC上的一点，试问当点E在什么位置时，直线ED与⊙O相切？请说明理由.

如图，已知半径为1的⊙与轴交于A、B两点，经过原点的直线MN切⊙ 于点M，圆心的坐标为（2，0）．

（1）求切线MN的函数解析式；
（2）线段上是否存在一点，使得以P、O、A为顶点的三角形与相似?若存在，请求出所有符合条件的点的坐标；若不存在，请说明理由．
（3）若将⊙沿着x轴的负方向以每秒1个单位的速度移动；同时将直线MN以每秒2个单位的速度向下平移，设运动时间为t（t＞0），求t为何值时，直线MN再一次与⊙相切？（本小题保留3位有效数字）

图1是某学校存放学生自行车的车棚的示意图（尺寸如图所示），车棚顶部是圆柱侧面的—部分，其展开图是矩形．图2是车棚顶部截面的示意图，AB所在圆的圆心为点O．

(1)求AB所在⊙O的半径OA的长；
(2)车棚顶部是用一种帆布覆盖的，求覆盖棚顶的帆布的面积（不考虑接缝等因素，计算结果保留π）．

如图，已知AB是⊙O的直径，AD⊥DC，弦AC平分∠DAB，

(1)求证：DC是⊙O的切线；
(2)若AD＝2，AC＝；，求AB的长．

如图所示，AB是⊙O的直径，弦BC=2cm，∠ABC=60º．

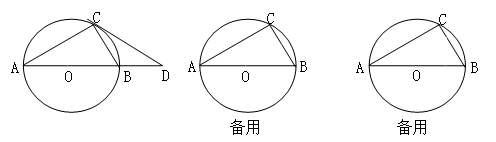
（1）求⊙O的直径；
（2）若D是AB延长线上一点，连结CD，当BD长为多少时，CD与⊙O相切；
（3）若动点E以2cm/s的速度从点A出发沿着AB方向运动，同时动点F以1cm/s的速度从点B出发沿BC方向运动，设运动时间为t(s)(0<t<2)，连结EF，当t为何值时，△BEF为直角三角形．

如图，已知CD是⊙O的直径，点A为CD延长线上一点，BC=AB，∠CAB=30°．

（1）求证：AB是⊙O的切线；
（2）若⊙O的半径为2，求弧BD的长

如图为圆柱形大型储油罐固定在U型槽上的横截面图．已知图中ABCD为等腰梯形（AB∥DC），支点A与B相距8m，罐底最低点到地面CD距离为1m．设油罐横截面圆心为O，半径为5m，∠D = 56°，求：（1）弧AB的度数（参考数据：sin53°≈0.8，tan56°≈1.5）
（2）U型槽的横截面（阴影部分）的面积．（参考数据：sin53°≈0.8，tan56°≈1.5，π≈3，结果保留整数）

将一根长为16厘米的细铁丝剪成两段，并把每段铁丝围成圆，设所得两圆半径分别为r和R，面积分别为S₁和S₂．
⑴ 求R与r的数量关系式，并写出r的取值范围；
⑵ 记S＝S₁＋S₂，求S关于r的函数关系式，并求出S的最小值．

如图，直线AE与以AB为直径的⊙O相切于点A，点C、D在⊙O上，并分别位于AB的两侧，∠EAC＝60°．

⑴ 求∠D的度数；
⑵ 当BC＝4时，求劣弧AC的长．