初中数学圆幂定理解答题

如图，在⊙O中，CD为⊙O的直径， =，点E为OD上任意一点(不与O、D重合).求证：AE=BE.

已知⊙O中，AC为直径，MA、MB分别切⊙O于点A、B．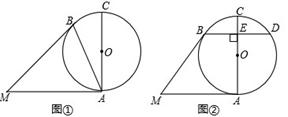

（1）如图①，若∠BAC=25°，求∠AMB的大小；
（2）如图②，过点B作BD⊥AC于E，交⊙O于点D，若BD=MA，求∠AMB的大小．

如图，在梯形中,，已知，点为边上的动点，连接，以为圆心，为半径的⊙分别交射线于点，交射线于点,交射线于，连接.
 
（1）求的长.
（2）当时，求的长.
（3）在点的运动过程中，
①当时，求⊙的半径.
②当时，求⊙的半径（直接写出答案）.

如图，AB是⊙O的直径，C是AB延长线上一点，CD与⊙O相切于点E，AD⊥CD于点D．

（1）求证：AE平分∠DAC；
（2）若AB=4，∠ABE=60°．
①求AD的长；
②求出图中阴影部分的面积.

如图，P是的⊙O半径OA上的一点，D在⊙O上，且PD=PO.过点D作⊙O的切线交OA的延长线于点C，延长DP交⊙O于K，连接KO、OD.

（1）证明：PC=PD；
（2）若该圆半径为5，CD//KO，请求出OC的长.

如图，AB是O的直径，C为AB延长线上一点，CD交O于点D，且∠A=∠C=30º.

（1）证明CD是的切线；
（2）请你写出线段BC和AC之间的数量关系，并证明.

已知:如图, BD是半圆O的直径,A是BD延长线上的一点，BC⊥AE，交AE的延长线于点C, 交半圆O于点E，且E为的中点.

（1）求证：AC是半圆O的切线；
（2）若，求的长．

如图，△ABC内接于⊙O，AB＝AC，BD是⊙O的直径， AD与BC交于点E，
F在DA的延长线上，且AF＝AE．

（1）试判断BF与⊙O的位置关系，并说明理由；
(2）若BF＝5，，求⊙O的直径．

如图，在Rt△ABC中，∠ACB=90°，AC=9cm，BC=12cm，P为BC的中点．动点Q从点P出发，沿射线PC方向以2cm/s的速度运动，以P为圆心，PQ长为半径作圆．设点Q运动的时间为t s．

（1）求点P到直线AB的距离；
（2）当t=1.8时，判断直线AB与⊙P的位置关系，并说明理由；
（3）已知⊙O为△ABC的外接圆，若⊙P与⊙O相切，求t的值．

如图，在⊙O中，直径AB=2，CA切⊙O于A，BC交⊙O于D，若∠C=45°，

（1）求BD的长；
（2）求阴影部分的面积.

如图，AB是⊙O的直径，弦DE垂直平分半径OA，C为垂足，DE=3，连结DB，过点E作EM∥BD，交BA的延长线于点M。

（1）求⊙O的半径；
（2）求证：EM是⊙O的切线；
（3）若弦DF与直径AB相交于点P，当∠DPA=45°时，求图中阴影部分的面积。

如图，AB是⊙O的直径，C是⊙O上一点，AD垂直于过C点的切线，垂足为D。

（1）求证：AC平分∠BAD；（2）若AC=，CD=2，求⊙O的直径。

如图，BC是⊙O的直径，A是弦BD延长线上一点，切线DE平分AC于E。

（1）求证：AC是⊙O的切线；
（2）若AD:DB=3:2，AC=15，求⊙O的直径。

如图，在单位长度为1的正方形网格中，一段圆弧经过格点A、B、C．

（1）请找出该圆弧所在圆的圆心O的位置；
（2）请在（1）的基础上，完成下列问题：
①⊙O的半径为_______（结果保留根号）；
②的长为_________（结果保留π）；
③试判断直线CD与⊙O的位置关系，并说明理由．

如图，已知AB是⊙O的直径，C是⊙O上一点，OD⊥BC于点D，过点C作⊙O
切线，交OD的延长线于点E，连结BE．

（1）求证：BE与⊙O相切；
（2）连结AD并延长交BE于点F，若OB＝6，且sin∠ABC＝，求BF的长．