如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,DE=3,连结DB,过点E作EM∥BD,交BA的延长线于点M。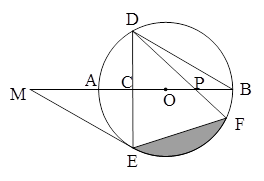
(1)求⊙O的半径;
(2)求证:EM是⊙O的切线;
(3)若弦DF与直径AB相交于点P,当∠DPA=45°时,求图中阴影部分的面积。
相关知识点
推荐套卷
如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,DE=3,连结DB,过点E作EM∥BD,交BA的延长线于点M。
(1)求⊙O的半径;
(2)求证:EM是⊙O的切线;
(3)若弦DF与直径AB相交于点P,当∠DPA=45°时,求图中阴影部分的面积。