如图，已知半径为1的⊙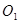
与
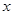轴交于A、B两点，经过原点的直线MN切⊙ 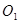于点M，圆心
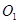的坐标为（2，0）．
（1）求切线MN的函数解析式；
（2）线段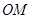
上是否存在一点
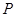，使得以P、O、A为顶点的三角形与
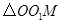相似?若存在，请求出所有符合条件的点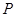的坐标；若不存在，请说明理由．
（3）若将⊙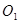沿着x轴的负方向以每秒1个单位的速度移动；同时将直线MN以每秒2个单位的速度向下平移，设运动时间为t（t＞0），求t为何值时，直线MN再一次与⊙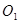相切？（本小题保留3位有效数字）
相关试题
A、B两地相距64千米，甲、乙两人分别从A、B两地骑车相向而行，且甲比乙晚出发40分钟．如果甲比乙骑车每小时多行4千米，那么两人恰好在AB中点相遇．求甲、乙两人骑车的速度各是多少千米/小时
的值，其中x=2005。”甲同学把“x=2005”错抄成 “x=2008”。但他的计算结果也是正确的。你说说这是怎么回事？
，所以
.
的取值范围.
如图1，在△ABC中，AB＝BC＝5，AC="6." △ECD是△ABC沿BC方向平移得到的，连接AE. AC和BE相交于点O.
⑴判断四边形ABCE是怎样的四边形，说明理由；
⑵如图2，P是线段BC上一动点，（不与点B、C重合），连接PO并延长交线段AB于点Q，QR⊥BD，垂足为点R.四边形PQED的面积是否随点P的运动而发生变化？若变化，请说明理由；若不变，求
出四边形PQED的面积.
相关知识点
推荐套卷
粤公网安备 44130202000953号