如图,△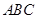 中,
中,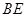 是它的角平分线,
是它的角平分线,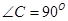 ,
,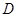 在
在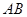 边上,以
边上,以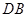 为直径的半圆
为直径的半圆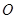 经过点
经过点 ,交
,交 于点
于点 。
。
(1)求证: 是
是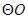 的切线;
的切线;
(2)若 ,连接
,连接 ,求证:
,求证: ∥
∥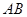 ;
;
(3)在(2)的条件下,若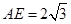 ,求图中阴影部分的面积。
,求图中阴影部分的面积。
相关知识点
推荐套卷
如图,△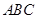 中,
中,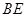 是它的角平分线,
是它的角平分线,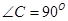 ,
,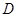 在
在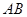 边上,以
边上,以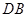 为直径的半圆
为直径的半圆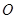 经过点
经过点 ,交
,交 于点
于点 。
。
(1)求证: 是
是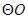 的切线;
的切线;
(2)若 ,连接
,连接 ,求证:
,求证: ∥
∥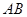 ;
;
(3)在(2)的条件下,若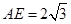 ,求图中阴影部分的面积。
,求图中阴影部分的面积。