[浙江]2013届浙江省宁波市九年级第三次质量分析数学试卷
已知抛物线 的开口向下,顶点坐标为(2,-3),那么该抛物线有( )
的开口向下,顶点坐标为(2,-3),那么该抛物线有( )
| A.最小值-3 | B.最大值-3 | C.最小值2 | D.最大值2 |
如图,A、B、C是⊙O上的三点,已知∠O=60º,则∠C=( )

A.20º B.25º C.30º D.45º
已知相似△ADE与△ABC的相似比为1:2,则△ADE与△ABC的面积比为( ).
| A.1:2 | B.1:4 | C.2:1 | D.4:1 |
一个不透明的布袋装有4个只有颜色不同的球,其中2个红色,1个白色,1个黑色,搅匀后从布袋里摸出1个球,摸到红球的概率是( )
A. |
B. |
C. |
D. |
已知圆 和圆
和圆 相切,两圆的圆心距为8cm,圆
相切,两圆的圆心距为8cm,圆 的半径为3cm,则圆
的半径为3cm,则圆 的半径是( )
的半径是( )
| A.5cm | B.11cm | C.3cm | D.5cm或11cm |
亮亮想制作一个圆锥模型,这个模型的侧面是用一个半径为9cm,圆心角为240°的扇形铁皮制作的,再用一块圆形铁皮做底。请你帮他计算这块圆形铁皮的半径为( )
| A.2cm; | B.3cm; | C.6cm; | D.12cm. |
下列四个命题:(1)全等的两个三角形相似;(2)有一个角相等的两个等腰三角形相似;(3)所有的等边三角形都相似;(4)所有的直角三角形都相似.其中真命题的个数有( )
| A.1个; | B.2个; | C.3个; | D.4个. |
将函数y=2x2的图象向右平行移动1个单位,再向上平移5个单位,可得到的抛物线是( )
A. |
B. |
C. |
D. |
如图,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积和为( )
A. cm2; cm2; |
B. cm2; cm2; |
C. cm2; cm2; |
D. cm2. cm2. |
.如图,半圆D的直径AB=4,与半圆O内切的动圆O1与AB切于点M,设⊙O1的半径为y,AM=x,则y关于x的函数关系式是 ( )
A.y=- x2+x x2+x |
B.y=-x2+x | C.y=- x2-x x2-x |
D.y= x2-x x2-x |
正方形ABCD中,有两个分别内接于△ABC,△ACD的小正方形,它们的面积分别为m,n(如图)则 =
= 
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线。如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,点D的坐标为(0,-3)AB为半圆直径,半圆圆心M(1,0),半径为2,则经过点D的“蛋圆”的切线的解析式为__________________。
如图,△ABC是格点三角形(三角形的三个顶点都是小正方形的顶点)。
(1)将△ABC绕点C逆时针旋转90°,得到△CDE.写出点B对应点D和点A对应点E的坐标。
(2) 若以格点P、A、B为顶点的三角形与△CDE相似但不全等,请写出符合条件格点P的坐标。
如图,已知二次函数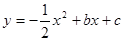 的图象经过A(2,0)、B(0,-6)两点。
的图象经过A(2,0)、B(0,-6)两点。
(1)求这个二次函数的解析式
(2)设该二次函数的对称轴与 轴交于点C,连结BA、BC,求△ABC的面积。
轴交于点C,连结BA、BC,求△ABC的面积。
不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,现从中任意摸出一个是白球的概率为 .
.
(1)求袋中蓝球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法,求两次摸到都是白球的概率.
如图:AB是⊙O的直径,D、T是圆上两点,且AT平分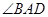 ,过点T作AD延长线的垂线PQ,垂足为C。
,过点T作AD延长线的垂线PQ,垂足为C。
求证:PQ是⊙O的切线。
若⊙O的半径为4,TC= ,求弦AD的长。
,求弦AD的长。
某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果以13元/千克的价格销售,那么每天可获取利润750元.
小红:通过调查验证,我发现每天的销售量y(千克)与销售单价x(元)之间存在一次函数关系.
(1)求y(千克)与x(元)(x>8)的函数关系式;
(2)当销售单价为何值时,该超市销售这种水果每天获取的利润达到800元?【利润=销售量×(销售单价-进价)】
(3)一段时间后,发现这种水果每天的销售量均不低于225千克.则此时该超市销售这种水果每天利润最大是多少?(x>8)
 ,则此函数图象也经过点( )
,则此函数图象也经过点( )



 中,
中,
 ,
, ,
, ,则下列结论正确的是( )
,则下列结论正确的是( )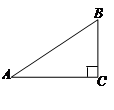

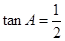
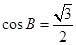

 (x≠0)的图象上,则m的值是 .
(x≠0)的图象上,则m的值是 .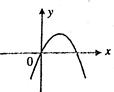
 |
| ;
; .
. ,并说明理由。
,并说明理由。

 ,求
,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号