[浙江]2012届浙江省湖州市环渚学校九年级上学期调研测试数学试卷
若反比例函数 的图象经过点(2,-3),则图象必经过另一点( )
的图象经过点(2,-3),则图象必经过另一点( )
| A.(2,3) | B.(-2,3) | C.(3,2) | D.(-2,-3) |
已知反比例函数 的图象上有两点A(6,y1)、B(5,y2),则y1与y2的大小关系为( )
的图象上有两点A(6,y1)、B(5,y2),则y1与y2的大小关系为( )
| A.y1>y2 | B.y1=y2 | C.y1<y2 | D.无法确定 |
下列函数的图象,一定经过原点的是( )
| A.y=x2-1 | B. y=3x2-2x | C.y=2x+1 | D.y= |
下列三个命题:①圆既是轴对称图形,又是中对称图形;②垂直于弦的直径平分这条弦;③相等圆心角所对的弧相等.其中是真命题的是( )
| A.①② | B.②③ | C.①③ | D.①②③ |
过⊙O内一点M的最长的弦为6cm, 最短的弦长为4cm, 则OM的长为 ( )
A.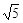 cm cm |
B.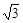 cm cm |
C.3cm | D.2cm |
如图,A、B、C是⊙O上的三点,∠BAC=30°,则∠BOC的大小是 ( )
A.60° B.45° C.30° D.15°
反比例函数 的图象如图所示,点M是该函数图象上一点,MN⊥x轴,垂足是点N,如果S△MON=2,则k的值为( )
的图象如图所示,点M是该函数图象上一点,MN⊥x轴,垂足是点N,如果S△MON=2,则k的值为( )
| A.2 | B.-2 | C.4 | D.-4 |
如图坐标平面上有一透明片,透明片上有一拋物线及一点P,且拋物线为二次函数y=x2的图形,P的坐标(2,4)。若将此透明片向右、向上移动后,得拋物线的顶点坐标为(7,2),则此时P的坐标为 ( ) 
| A.(9,4) | B.(9,6) | C.(10,4) | D.(10,6) |
某校举行第15届校田径运动会,九年级甲、乙两位同学报名参加了男子铅球项目.已知甲、乙两位同学获得最好成绩时铅球行进的高度y(m)与水平距离x(m)之间的关系分别是 、
、 ,那么在这次比赛中,成绩较好的学生是( )
,那么在这次比赛中,成绩较好的学生是( )
| A.甲 | B.乙 | C.甲、乙成绩相同 | D.无法比较 |
半径为2cm 的⊙O中有长为2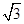 cm的弦AB,则弦AB所对的圆周角度数为( )
cm的弦AB,则弦AB所对的圆周角度数为( )
| A.600 | B.900 | C.600或1200 | D.450或900 |
已知二次函数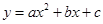 的图象与
的图象与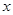 轴交于点
轴交于点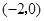 、
、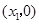 ,且
,且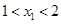 ,与
,与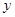 轴的正半轴的交点在
轴的正半轴的交点在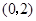 的下方.下列结论:①
的下方.下列结论:①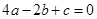 ;②
;②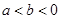 ;③
;③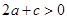 ;④
;④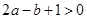 .其中正确结论的个数是 个。 ( )
.其中正确结论的个数是 个。 ( )
| A.1 | B.2 | C.3 | D.4 |
日常生活中,“老人”是一个模糊概念.有人想用“老人系数”来表示一个人的老年化程度.他设想“老人系数”的计算方法如表:
| 人的年龄x(岁) |
x≤60 |
60<x<80 |
x≥80 |
| 该人的“老人系数” |
0 |
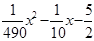 |
1 |
按照这样的规定,一个70岁的人的“老人系数”为 。
如图,平行于y轴的直线L被抛物线y= 、y=
、y=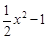 所截.当直线L向右平移2个单位时,直线L被两条抛物线所截得的线段扫过的图形面积为 __ 平方单位。
所截.当直线L向右平移2个单位时,直线L被两条抛物线所截得的线段扫过的图形面积为 __ 平方单位。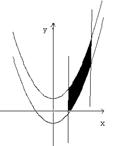
(8分)如图,A、B两点在函数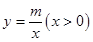 的图象上.(1)求
的图象上.(1)求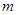 的值及直线AB的解析式; (2)如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.请直接写出图中阴影部分(不包括边界)中所有格点的坐标。
的值及直线AB的解析式; (2)如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.请直接写出图中阴影部分(不包括边界)中所有格点的坐标。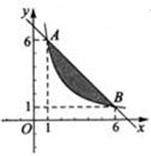
(8分)如图,AB、CD为⊙O内两条相交的弦,交点为E,且AB=CD。则以下结论中:①AE=EC ②AD=BC ③BE=EC ④AD∥BC, 正确的有 。试证明你的结论。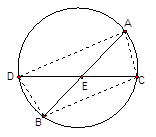
(10分) 如图,已知抛物线y = ax2-x + c经过点Q(-2,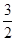 ),且它的顶点P的横坐标为-1.设抛物线与x轴相交于A、B两点。
),且它的顶点P的横坐标为-1.设抛物线与x轴相交于A、B两点。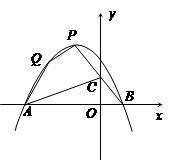
(1)求抛物线的解析式及顶点P的坐标;
(2)求A、B两点的坐标;并求当x为何值时,y>0?
(3)设PB交y轴于C点,求线段PC的长。
(10分)某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面。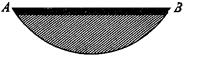 (1)请你用直尺和圆规补全这个输水管道的圆形截面(保留作图痕迹);
(1)请你用直尺和圆规补全这个输水管道的圆形截面(保留作图痕迹);
(2)若这个输水管道有水部分的水面宽AB=14cm,水面最深地方的高度为5cm,求这个圆形截面的半径。
“快乐购”超市购进一批25元/千克的绿色食品,如果以30元/千克销售,那么每天可售出400千克.由销售经验知,每天销售量y(千克)与销售单价x(元)(x≥30)存在如图所示的一次函数关系式。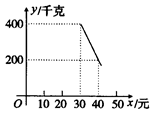
(1)试求出y与x的函数关系式;
(2)设“快乐购”超市销售该绿色食品每天获得利润P元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
(3)根据市场调查,该绿色食品每天可获利润不超过3080元,现该超市经理要求每天利润不得低于3000元,请你帮助该超市确定绿色食品销售单价x的范围(直接写出答案)。
如图,顶点为D的抛物线 与x轴相交于A、B两点,与y轴相交于点C,连结BC,已知△BOC是等腰三角形。
与x轴相交于A、B两点,与y轴相交于点C,连结BC,已知△BOC是等腰三角形。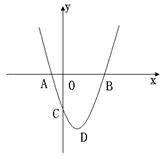
(1)求点B的坐标及抛物线 的解析式;
的解析式;
(2)求四边形ACDB的面积;
(3)若点E(x,y)是y轴右侧的抛物线上不同于点B的任意一点,设以A,B,C,E为顶点的四边形的面积为S。①求S与x之间的函数关系式。②若以A,B,C,E为顶点的四边形与四边形ACDB的面积相等,求点E的坐标。
已知一个等腰三角形纸片放在桌面上,它的三边长分别为5cm、5cm、6cm,若要用一个圆形纸片把这个三角形纸片完全盖住,那么这个圆形纸片的面积最小是 。
 的解的个数是( )
的解的个数是( ) 的图像位于第二、四象限,则k的值可以是 (写出满足条件的一个k的值即可)。
的图像位于第二、四象限,则k的值可以是 (写出满足条件的一个k的值即可)。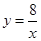 ,若x≤2时,则y的取值范围是_ __。
,若x≤2时,则y的取值范围是_ __。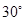 ,AB=8,则⊙O的直径为 。
,AB=8,则⊙O的直径为 。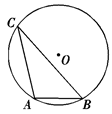
 的图象上,△OP1A1,△P2A1A2,△P3A2A3……△PnAn-1An……都是等腰直角三角形,斜边OA1,A1A2……An-1An,都在x轴上, 则y1+y2+…yn= 。
的图象上,△OP1A1,△P2A1A2,△P3A2A3……△PnAn-1An……都是等腰直角三角形,斜边OA1,A1A2……An-1An,都在x轴上, 则y1+y2+…yn= 。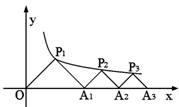
 粤公网安备 44130202000953号
粤公网安备 44130202000953号