如图,已知一次函数 的图象经过点A(2,3),AB⊥x轴,垂足为B,连接OA.
的图象经过点A(2,3),AB⊥x轴,垂足为B,连接OA.
(1)求此一次函数的解析式,并求出一次函数与x轴的交点C的坐标;
(2)设点P为直线 在第一象限内的图像上的一动点,求△OBP的面积S与x之间的函数关系式,并写出自变量x的范围;
在第一象限内的图像上的一动点,求△OBP的面积S与x之间的函数关系式,并写出自变量x的范围;
(3)设点M为坐标轴上一点,且 ,直接写出所有满足条件的点M的坐标.
,直接写出所有满足条件的点M的坐标.
甲、乙两人沿相同的路线由A到B匀速行进,A、B两地间的距离为20km.他们行进的路程s(km)与甲出发后的时间t(h)之间的函数图象如图所示.
(1)甲走完全程所用的时间为 小时;
(2)乙行走的速度为 ;
(3)当乙行走了多少时间,他们两人在途中相遇?
(本题12分)如图,过点A(0,3)的直线l1与x轴交于点B,tan∠ABO= .过点A的另一直线l2:y=-
.过点A的另一直线l2:y=- x+b (t>0)与x轴交于点Q,点P是射线AB上的一个动点,过P作PH⊥x轴于点H,设PB=5t.
x+b (t>0)与x轴交于点Q,点P是射线AB上的一个动点,过P作PH⊥x轴于点H,设PB=5t.
(1)求直线l1 的函数解析式;
(2)当点P在线段AB上运动时,设△PHQ的面积为S(S≠0),求S与t之间的函数关系式(要求写出自变量t的取值范围);
(3)当点P 在射线AB上运动时,是否存在这样的t值,使以P,H,Q为顶点的三角形与△AOQ相似?若存在,直接写出所有满足条件的t值所对应的P点坐标;若不存在,请说明理由.
(本题12分)如图1,已知在直角坐标系XOY中,正△OBC的边长和等腰直角△DEF的底边都为6,点E与坐标原点O重合,点D、B在X轴上,连结FC,在△DEF沿X轴的正方向以每秒 个单位运动时,边EF所在直线和边OC所在直线相交于G,设运动时间为t.
个单位运动时,边EF所在直线和边OC所在直线相交于G,设运动时间为t.
(1)如图2,当t=1时,①求OE的长;②求∠FGC的度数;③求G点坐标;
(2)①如图3,当t为多少时,点F恰在△OBC的OC边上;
②在点F、C、G三点不共线时,记△FCG的面积为S,用含t的代数式表示S,并写出t的相应取值范围.
某地为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过12吨(含12吨)时,每吨按政府补贴优惠价收费;每月超过12吨,超过部分每吨按市场调节价收费,小黄家1月份用水24吨,交水费42元.2月份用水20吨,交水费32元.
(1)求每吨水的政府补贴优惠价和市场调节价分别是多少元;
(2)设每月用水量为x吨,应交水费为y元,写出y与x之间的函数关系式;
(3)小黄家3月份用水26吨,他家应交水费多少元?
如图,在平面直角坐标系中,⊙M过原点O,与x轴交于A(4,0),与y轴交于B(0,3),点C为劣弧AO的中点,连接AC并延长到D,使DC=4CA,连接BD.
(1)求⊙M的半径;
(2)证明:BD为⊙M的切线;
(3)在直线MC上找一点P,使|DP﹣AP|最大.
一水果经销商购进了A,B两种水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如下表:
(1)如果甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱,请你计算出经销商能盈利多少元?
(2)在甲、乙两店各配货10箱(按整箱配送),且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
如图,在平面直角坐标系中,四边形ABCD是菱形,B、O在x轴负半轴上,AO=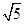 ,tan∠AOB=
,tan∠AOB=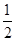 ,一次函数
,一次函数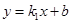 的图象过A、B两点,反比例函数
的图象过A、B两点,反比例函数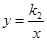 的图象过OA的中点D.
的图象过OA的中点D.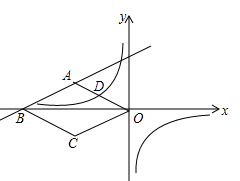
(1)求一次函数和反比例函数的表达式;
(2)平移一次函数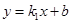 的图象,当一次函数
的图象,当一次函数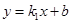 的图象与反比例函数
的图象与反比例函数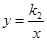 的图象无交点时,求b的取值范围.
的图象无交点时,求b的取值范围.
为了发展旅游经济,我市某风景区对门票采用灵活的售票方法吸引游客,门票的定价为每人50元,,非节日打a折售票,节假日按团队人数分段定价售票,即m人一下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人的部分的游客打b折售票,设某旅游团人数为x人,非节假日购票款为y (元),节假日购票款为y
(元),节假日购票款为y (元)。y
(元)。y 、y
、y 与x之间的函数图像如图所示
与x之间的函数图像如图所示
(1)观察图像可知a= ,b= ,m=
(2)直接写出y , y
, y 与x之间的函数解析式
与x之间的函数解析式
(3)某旅行社导游王娜于5月1日带A团,5月20日(非节假日)带B团到该景区旅游,共付门票款1900元,A、B两个团队合计50人,求A、B两个团队各有多少人?
已知:二次函数y=ax2+bx-2的图象经过点(1,0),一次函数图象经过原点和点(1,-b),其中a>b>0且a、b为实数.
(1)求一次函数的表达式(用含b的式子表示);
(2)试说明:这两个函数的图象交于不同的两点;
(3)设(2)中的两个交点的横坐标分别为x1、x2,求|x1-x2|的范围.
购进某种干果,由于销售状况良好,超市又用9000元第二次购进该干果,但第二次的进价比第一次的提髙了20%,第二次购进干果数量是第一次的2倍还多300千克.
(1)求该干果的第一次进价是每千克多少元?
(2)百姓超市按每千克9元的价格出售,当大部分干果售出后,余下的按售价的8折售完,若两次销售这种干果的利润不少于5820元,则最多余下多少千克干果按售价的8折销售.
如图1,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A、C分别在x轴、y轴的正半轴上,且OA=2,OC=1,矩形对角线AC、OB相交于E,过点E的直线与边OA、BC分别相交于点G、H.
(1)①直接写出点E的坐标: .
②求证:AG=CH.
(2)如图2,以O为圆心,OC为半径的圆弧交OA与D,若直线GH与弧CD所在的圆相切于矩形内一点F,求直线GH的函数关系式.
(3)在(2)的结论下,梯形ABHG的内部有一点P,当⊙P与HG、GA、AB都相切时,求⊙P的半径.
如图,一次函数 的图像与反比例函数
的图像与反比例函数 的图像交于
的图像交于 两点,与
两点,与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,已知
,已知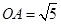 ,点
,点 的坐标为
的坐标为 ,过点
,过点 作
作 轴,垂足为
轴,垂足为 。
。
(1)求反比例函数和一次函数的解析式;
(2)求 的面积。
的面积。
(3)根据图像回答:当x 为何值时,一次函数的函数值大于
反比例函数的函数值?