初中数学一次函数的最值解答题

如图，已知直线AB分别交x轴、y轴于点A（﹣4，0）、B（0，3），点P从点A出发，以每秒1个单位的速度沿直线AB向点B移动，同时，将直线以每秒0．6个单位的速度向上平移，分别交AO、BO于点C、D，设运动时间为t秒（0＜t＜5）．
（1）证明：在运动过程中，四边形ACDP总是平行四边形；
（2）当t取何值时，四边形ACDP为菱形？且指出此时以点D为圆心，以DO长为半径的圆与直线AB的位置关系，并说明理由．

某酒厂生产A，B两种品牌的酒，每天两种酒共生产700瓶，每种酒每瓶的成本
和利润如下表所示，设每天共获利y元，每天生产A种品牌的酒x瓶．
（1）请写出y关于x的关系式；
（2）如果该厂每天至少投入成本30000元，那么每天至少获利多少元？
（3）要使每天的利润率最大，应生产A，B两种酒各多少瓶？

	A	B
成本（元）	50	35
利润（元）	20	15

 

如图，在平面直角坐标系中，正方形ABCD的顶点A在y轴正半轴上，顶点B在x轴正半轴上，OA、OB的长分别是一元二次方程x²﹣7x+12=0的两个根（OA＞OB）．
（1）求点D的坐标．
（2）求直线BC的解析式．
（3）在直线BC上是否存在点P，使△PCD为等腰三角形？若存在，请直接写出点P的坐标；若不存在，说明理由．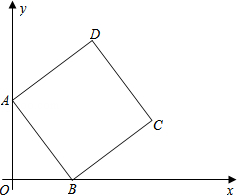

如图1，在等腰梯形ABCO中，AB∥CO，E是AO的中点，过点E作EF∥OC交BC于F，AO=4，OC=6，∠AOC=60°.现把梯形ABCO放置在平面直角坐标系中，使点O与原点重合，OC在x轴正半轴上，点A，B在第一象限内．
（1）求点E的坐标及线段AB的长；
（2）点P为线段EF上的一个动点，过点P作PM⊥EF交OC于点M，过M作MN∥AO交折线ABC于点N，连结PN,设PE=x.△PMN的面积为S.
①求S关于x的函数关系式；
②△PMN的面积是否存在最大值，若不存在，请说明理由.若存在，求出面积的最大值；

（3）另有一直角梯形EDGH（H在EF上，DG落在OC上，∠EDG=90°，且DG=3，HG∥BC.现在开始操作：固定等腰梯形ABCO，将直角梯形EDGH以每秒1个单位的速度沿OC方向向右移动，直到点D与点C重合时停止（如图2）.设运动时间为t秒，运动后的直角梯形为E′D′G′H′（如图3）;试探究：在运动过程中，等腰梯ABCO与直角梯形E′D′G′H′重合部分的面积y与时间t的函数关系式.

如图，在平面直角坐标系中，直线AB与x轴、y轴分别交于点A，B，直线CD与x轴、y轴分别交于点C，D，AB与CD相交于点E，线段OA，OC的长是一元二次方程x²﹣18x+72=0的两根（OA＞OC），BE=5，tan∠ABO=．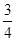
（1）求点A，C的坐标；
（2）若反比例函数y=的图象经过点E，求k的值；
（3）若点P在坐标轴上，在平面内是否存在一点Q，使以点C，E，P，Q为顶点的四边形是矩形？若存在，请写出满足条件的点Q的个数，并直接写出位于x轴下方的点Q的坐标；若不存在，请说明理由．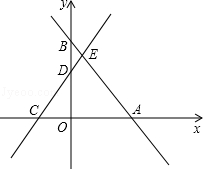

如图1，在平面直角坐标系xOy中，等腰直角△AOB的斜边OB在x上，顶点A的坐标为（3，3）.
（1）求直线OA的解析式；
（2）如图2，如果点P是x轴正半轴上的一个动点，过点P作PC∥y轴，交直线OA于点C，设点P的坐标为（m，0），以A、C、P、B为顶点的四边形面积为S，求S与m之间的函数关系式；
（3）如图3，如果点D（2，a）在直线AB上. 过点O、D作直线OD，交直线PC于点E，在CE的右侧作矩形CGFE，其中CG=，请你直接写出矩形CGFE与△AOB重叠部分为轴对称图形时m的取值范围.

图1                     图2                       图3

如图，在等腰△ABC中，AB=AC=5，BC=6，点D为BC边上一动点（不与点B重合），过D作射线DE交AB边于E，使∠BDE=∠A，以D为圆心、DC的长为半径作⊙D．
（1）设BD=x，AE=y，求y关于x的函数关系式，并写出定义域．
（2）当⊙D与AB边相切时，求BD的长．
（3）如果⊙E是以E为圆心，AE的长为半径的圆，那么当BD的长为多少时，⊙D与⊙E相切？

如图，在平面直角坐标系中，正方形OABC的边长为a．直线y=bx+c交x轴于E，交y轴于F，且a、b、c分别满足-(a-4)²≥0，
（1）求直线y=bx+c的解析式并直接写出正方形OABC的对角线的交点D的坐标；
（2）直线y=bx+c沿x轴正方向以每秒移动1个单位长度的速度平移，设平移的时间为t秒，问是否存在t的值，使直线EF平分正方形OABC的面积？若存在，请求出t的值；若不存在，请说明理由；
点P为正方形OABC的对角线AC上的动点（端点A、C除外），PM⊥PO，交直线AB于M，求的值

甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地，乙车比甲车晚出发2小时(从甲车出发时开始计时)．图中折线、线段分别表示甲、乙两车所行路程(千米)与时间(小时)之间的函数关系对应的图象(线段表示甲出发不足2小时因故停车检修)．请根据图象所提供的信息，解决如下问题：

(1)求乙车所行路程与时间的函数关系式；
(2)求两车在途中第二次相遇时，它们距出发地的路程；
(3)乙车出发多长时间，甲、乙两车相距80千米？(写出解题过程)

为响应环保组织提出的“低碳生活”的号召，李明决定不开汽车而改骑自行车上班．有一天，李明骑自行车从家里到工厂上班，途中因自行车发生故障，修车耽误了一段时间，车修好后继续骑行，直至到达工厂（假设在骑自行车过程中匀速行驶）．李明离家的距离y（米）与离家时间x（分钟）的关系表示如下图：

李明从家出发到出现故障时的速度为         米／分钟；
李明修车用时           分钟；
求线段BC所对应的函数关系式（不要求写出自变量的取值范围）．

如图，在平面直角坐标系中，四边形OABC的顶点O是坐标原点，点A在第一象限，点C在第四象限，点B的坐标为（60，0），OA=AB，∠OAB=90°，OC=50．点P是线段OB上的一个动点（点P不与点O、B重合），过点P与y轴平行的直线l交边OA或边AB于点Q，交边OC或边BC于点R，设点P横坐标为t，线段QR的长度为m．已知t=40时，直线l恰好经过点C．

（1）求点A和点C的坐标；
（2）当0＜t＜30时，求m关于t的函数关系式；
（3）当m=35时，请直接写出t的值；
（4）直线l上有一点M，当∠PMB+∠POC=90°，且△PMB的周长为60时，请直接写出满足条件的点M的坐标．

如图，矩形OABC摆放在平面直角坐标系xOy中，点A在x轴上，点C在y轴上，OA=3，OC=2，P是BC边上一点且不与B重合，连结AP，过点P作∠CPD=∠APB，交x轴于点D，交y轴于点E，过点E作EF∥AP交x轴于点F．
（1）若△APD为等腰直角三角形，求点P的坐标；
（2）若以A，P，E，F为顶点的四边形是平行四边形，求直线PE的解析式．

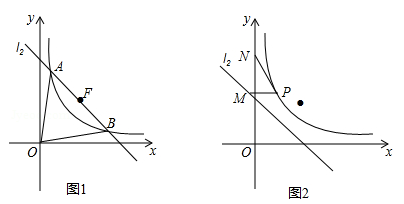
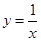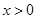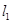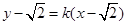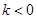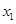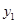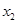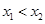（黄石）已知双曲线（），直线：（k＜0）过定点F且与双曲线交于A，B两点，设A（，），B（，）（），直线：．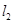

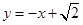（1）若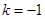，求△OAB的面积S；
（2）若AB=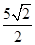，求k的值；
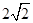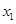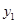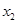（3）设N（0，），P在双曲线上，M在直线l₂上且PM∥x轴，求PM+PN最小值，并求PM+PN取得最小值时P的坐标．（参考公式：在平面直角坐标系中，若A（，），B（，）则A，B两点间的距离为AB=．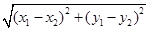

直线与x轴交于点A，与y轴交于点B，菱形ABCD如图放置在平面直角坐标系中，其中点D在x轴负半轴上，直线y=x+m经过点C，交x轴于点E．
①请直接写出点C、点D的坐标，并求出m的值；
②点P（0，t）是线段OB上的一个动点（点P不与O、B重合），经过点P且平行于x轴的直线交AB于M、交CE于N．设线段MN的长度为d，求d与t之间的函数关系式（不要求写自变量的取值范围）；
③点P（0，t）是y轴正半轴上的一个动点，为何值时点P、C、D恰好能组成一个等腰三角形？

某零件制造车间有工人20名，已知每名工人每天可制造甲种零件6个或乙种零件5个，且每制造一个甲种零件，可获利润150元，每制造一个乙种零件可获利润260元，在这20名工人中，车间每天安排x名工人制造甲种零件，其余工人制造乙种零件，且生产乙种零件的个数不超过甲种零件个数的一半．
（1）请写出此车间每天所获利润y（元）与x（人）之间的函数关系式；
（2）求自变量x的取值范围；
（3）怎样安排生产，每天获得的利润最大，最大利润是多少？