初中数学一次函数的最值解答题

经过点（1，1）的直线l：与反比例函数G_1:的图象交于点，B（b，-1），与y轴交于点D．
（1）求直线l对应的函数表达式及反比例函数G₁的表达式；
（2）反比例函数G_2::，
①若点E在第一象限内，且在反比例函数G₂的图象上，若EA=EB，且△AEB的面积为8，求点E的坐标及t值；
②反比例函数G₂的图象与直线l有两个公共点M，N（点M在点N的左侧），若，直接写出t的取值范围．

在直角坐标系中，设x轴为直线l，函数的图像分别是，半径为1的与直线中的两条相切，例如是其中一个的圆心坐标.
（1）写出其余满足条件的的圆心坐标；
（2）在图中标出所有圆心，并用线段依次连接各圆心，求所得几何图形的周长.

如图，已知抛物线经过O(0,0)，A(4,0),B(3,)三点，连接AB，过点B作BC∥轴交该抛物线于点C.

求这条抛物线的函数关系式.
两个动点P、Q分别从O、A同时出发,以每秒1个单位长度的速度运动. 其中，点P沿着线段0A向A点运动，点Q沿着线段AB向B点运动. 设这两个动点运动的时间为（秒) (0＜≤2)，△PQA的面积记为S.
① 求S与的函数关系式；
② 当为何值时，S有最大值，最大值是多少？并指出此时△PQA的形状；
是否存在这样的值，使得△PQA是直角三角形?若存在，请直接写出此时P、Q两点的坐标；若不存在，请说明理由.

某商场要经营一种新上市的文具，进价为20元/件．试营销阶段发现：当销售单价是25元时，每天的销售量为250件；销售单价每上涨1元，每天的销售量就减少10件．
（1）写出商场销售这种文具，每天所得的销售利润w（元）与销售单价x（元）之间的函数关系式；
（2）求销售单价为多少元时，该文具每天的销售利润最大；
（3）商场的营销部结合上述情况，提出了A、B两种营销方案：
方案A：该文具的销售单价高于进价且不超过30元；
方案B：每天销售量不少于10件，且每件文具的利润至少为25元
请比较哪种方案的最大利润更高，并说明理由．

如图，已知反比例函数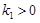（）与一次函数 （）相交于A、B两点，AC⊥轴于点C．若△OAC的面积为1，且tan∠AOC=2．
（1）求出反比例函数与一次函数的解析式；
（2）请直接写出B点的坐标，并指出当为何值时，反比例函数的值大于一次函数的值？

如图①，在矩形 ABCD中，AB＝10cm，BC＝8cm．点P从A出发，沿A→B→C→D路线运动，到D停止；点Q从D出发，沿 D→C→B→A路线运动，到A停止．若点P、点Q同时出发，点P的速度为每秒1cm，点Q的速度为每秒2cm，a秒时点P、点Q同时改变速度，点P的速度变为每秒bcm，点Q的速度变为每秒dcm．图②是点P出发x秒后△APD的面积S₁（cm²）与x（秒）的函数关系图象；图③是点Q出发x秒后△AQD的面积S₂（cm²）与x（秒）的函数关系图象．

（1）参照图象，求b、图②中c及d的值；
（2）连接PQ，当PQ平分矩形ABCD的面积时，运动时间x的值为         ；
（3）当两点改变速度后，设点P、Q在运动线路上相距的路程为y（cm），求y（cm）与运动时间x（秒）之间的函数关系式，并写出自变量x的取值范围；
（4）若点P、点Q在运动路线上相距的路程为25cm，求x的值．

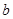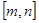设，是任意两个不等实数，我们规定：满足不等式≤≤的实数的所有取值的全体叫做闭区间，表示为. 对于一个函数，如果它的自变量与函数值满足：当m≤≤n时，有m≤≤n，我们就称此函数是闭区间上的“闭函数”.
（1）反比例函数是闭区间上的“闭函数”吗？请判断并说明理由；
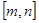（2）若一次函数是闭区间上的“闭函数”，求此函数的表达式；
（3）若二次函数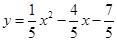是闭区间上的“闭函数”，直接写出实数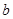， 的值.

如图①，将□ABCD置于直角坐标系中，其中BC边在x轴上（B在C的左边），点D坐标为（0,4），直线MN：沿着x轴的负方向以每秒1个单位的长度平移，设在平移过程中该直线被□ABCD截得的线段长度为m，平移时间为t，m与t的函数图像如图②所示．
（1）填空：点C的坐标为   ；
在平移过程中，该直线先经过B、D中的哪一点？   ；（填“B”或“D”）
（2）点B的坐标为   ，n＝   ，a＝   ；
（3）求图②中线段EF的解析式；
（4）t为何值时，该直线平分□ABCD的面积？

（1）如图1，等腰Rt△ABO放在平面直角坐标系中， 点A，B 的坐标分别是A（0，1），B（1，0）．在x轴正半轴上取D（m，0），在AD右上方作等腰Rt△ADE，∠ADE=．

①求出E点的坐标（可用含m的代数式表示）；
②证明对于任意正数m，点E都在直线上；
（2）将（1）中的两个等腰直角三角形都改为有一个角为的直角三角形，如图22-2，A（0，），B（1，0）．Rt△ADE中， ∠ADE=，∠AED=．D（m，0）是x轴正半轴上任意一点，则不论m取何正数，点E都在某一条直线上，请求出这条直线的函数关系式；
（3）将（2）中Rt△AOB保持不动，取点C（2， ），在x轴正半轴上取D（m，0）（m>2）， 然后在AD右上方作Rt△CDE， ∠CDE=，∠CED=．当m取不同值时，点E是否还是总在一条直线上? 若是，请求出直线对应的函数关系式，若不是，请说明理由．

对于平面直角坐标系中的任意两点P₁（x₁，y₁），P₂（x₂，y₂），我们把叫做P₁、P₂两点间的直角距离，记作d（P₁，P₂）．
（1）已知O为坐标原点，动点P（x，y）满足d（O，P）=1，请写出x与y之间满足的关系式，并在所给的直角坐标系中画出所有符合条件的点P所组成的图形；
（2）设P₀（x₀，y₀）是一定点，Q（x，y）是直线y=ax+b上的动点，我们把d（P0，Q）的最小值叫做P0到直线y=ax+b的直角距离．试求点M（2，1）到直线y=x+2的直角距离．

如图1，在平面直角坐标系中，已知点A（－6，0），点B（0，8），点C在y轴上，将△OAB沿直线AC对折，使点O落在边AB上的点D处．

（1）求直线AB、AC的解析式．
（2）如图2，过B作BE⊥AC，垂足为E，若F为AB边上一动点，是否存在点F，使C为△EOF内心，若存在，请求出F点坐标，若不存在，请说明理由．

已知：关于x的一元二次方程mx²﹣（4m+1）x+3m+3="0" （m＞1）．
（1）求证：方程有两个不相等的实数根；
（2）设方程的两个实数根分别为x₁，x₂（其中x₁＞x₂），若y是关于m的函数，且y=x₁﹣3x₂，求这个函数的解析式；
（3）将（2）中所得的函数的图象在直线m=2的左侧部分沿直线m=2翻折，图象的其余部分保持不变，得到一个新的图象．请你结合这个新的图象回答：当关于m的函数y=2m+b的图象与此图象有两个公共点时，b的取值范围．

一次函数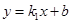的图象经过A（0，﹣2），B（1，0）两点，与反比例函数 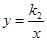的图象在第一象限内的交点为M（m，4）．
（1）求一次函数和反比例函数的表达式；
（2）在x轴上是否存在点P，使AM⊥MP？若存在，求出点P的坐标；若不存在，说明理由．

在平面直角坐标系xOy中，对于任意两点P₁（x₁，y₁）与P₂（x₂，y₂）的“非常距离”，给出如下定义：
若|x₁﹣x₂|≥|y₁﹣y₂|，则点P₁与点P₂的“非常距离”为|x₁﹣x₂|；
若|x₁﹣x₂|＜|y₁﹣y₂|，则点P₁与点P₂的“非常距离”为|y₁﹣y₂|．
例如：点P₁（1，2），点P₂（3，5），因为|1﹣3|＜|2﹣5|，所以点P₁与点P₂的“非常距离”为|2﹣5|=3，也就是图1中线段P₁Q与线段P₂Q长度的较大值（点Q为垂直于y轴的直线P₁Q与垂直于x轴的直线P₂Q交点）．
（1）已知点A（﹣，0），B为y轴上的一个动点，
①若点A与点B的“非常距离”为2，写出一个满足条件的点B的坐标；
②直接写出点A与点B的“非常距离”的最小值；
（2）已知C是直线y=x+3上的一个动点，
①如图2，点D的坐标是（0，1），求点C与点D的“非常距离”的最小值及相应的点C的坐标；
②如图3，E是以原点O为圆心，1为半径的圆上的一个动点，求点C与点E的“非常距离”的最小值及相应的点E与点C的坐标．

已知：如图，在平面直角坐标系xOy中，直线与x轴、y轴分别交于点A、B，点C在线段AB上，且．
（1）求点C的坐标（用含有m的代数式表示）；
（2）将△AOC沿x轴翻折，当点C的对应点C′恰好落在抛物线上时，求该抛物线的表达式；
（3）设点M为（2）中所求抛物线上一点，当以A、O、C、M为顶点的四边形为平行四边形时，请直接写出所有满足条件的点M的坐标．