如图①，将□ABCD置于直角坐标系中，其中BC边在x轴上（B在C的左边），点D坐标为（0,4），直线MN：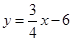
沿着x轴的负方向以每秒1个单位的长度平移，设在平移过程中该直线被□ABCD截得的线段长度为m，平移时间为t，m与t的函数图像如图②所示．
（1）填空：点C的坐标为 ；
在平移过程中，该直线先经过B、D中的哪一点？ ；（填“B”或“D”）
（2）点B的坐标为 ，n＝ ，a＝ ；
（3）求图②中线段EF的解析式；
（4）t为何值时，该直线平分□ABCD的面积？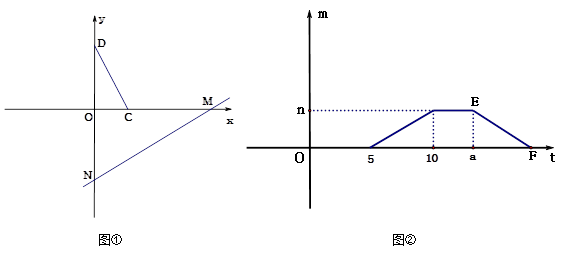
相关试题
如图，杂技团进行杂技表演，演员从跷跷板右端A处弹跳到人梯顶端椅子B处，其身体(看成一点)的路线是抛物线y=-
x2+3x+1的一部分，
(1)求演员弹跳离地面的最大高度；
(2)已知人梯高BC=3.4米，在一次表演中，人梯到起跳点A的水平距离是4米，问这表是
是否成功?请说明理由．
已知抛物线y＝－
x2＋x+
(1)该抛物线的对称轴是________，顶点坐标________；
(2)不列表在右上图的直角坐标系内描点画出该抛物线的图象，并且观察抛物线写出y <0时，x的取值范围；
(3)请问(2)中的抛物线经过怎样平移就可以得到y=ax2的图象？
(4)若该抛物线上两点A(x1，y1)、B(x2，y2)的横坐标满足x1>x2>1，试比y1与y2的大小
相关知识点
推荐套卷
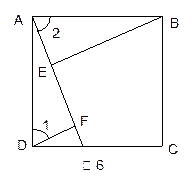
粤公网安备 44130202000953号