小张骑车往返于甲、乙两地，距甲地的路程
（千米）与时间
（小时）的函数图象如图所示．
（1）小张在路上停留 小时，他从乙地返回时骑车的速度为 千米／时．
（2）小王与小张同时出发，按相同路线前往乙地，距甲地的路程（千米）与时间（小时）的函数关系式为
．小王与小张在途中共相遇几次？请你计算第一次相遇的时间．
如图，直线
的解析式为
，且与
轴交于点
，直线
经过点
、
，直线、交于点
．
（1）求点的坐标；
（2）求直线的解析表达式；
（3）求
的面积；
（4）在直线上存在异于点的另一点
，使得
与的面积相等，请直接写出点的坐标．
如图，直线y=
x+2与x轴、y轴分别交于A、B两点，点C的坐标为（﹣3，0），P（x，y）是直线y=
x+2的一个动点（点P不与点A重合）．
（1）在点P运动过程中，试写出△OPC的面积S与x的函数关系式；
（2）当P运动到什么位置时，△OPC的面积为
，求出此时点P的坐标；
（3）过P作AB的垂线分别交x轴、y轴于E、F两点，是否存在这样的点P，使△EOF≌△BOA？若存在，求出点P的坐标；若不存在，请说明理由．
某地出租车计费方法如图，x（km）表示行驶里程，y（元）表示车费，请根据图象解答下列问题：
（1）该地出租车的起步价是_______元；
（2）当x＞2时，求y与x之间的函数关系式；
（3）若某乘客有一次乘出租车的里程为18km，则这位乘客需付出租车车费多少元？
已知如图，在平面直角坐标系中，一次函数
=
＋b（≠0）的图象与反比例函数=
（
≠0）的图象交于一、三象限内A、B两点，与轴交于点C；点A（2，m），点B（n，－2），且tn∠Boc=
；
（1）求一次函数和反比例函数的解析式；
（2）在轴上有一点E（O点除外），使得△BCE与△BCO的面积相等，求点E的坐标。
大星发超市进了一批成本为8元/个的文具盒。调查发现：这种文具盒每个星期的销售量y（个）与它的定价x（元/个）的关系如图所示：
（1）求这种文具盒每个星期的销售量y（个）与它的定价x（元/个）之间的函数关系式（不必写出自变
量x的取值范围）；
（2）每个文具盒定价是多少元时，超市每星期销售这种文具盒（不考虑其他因素）可获得的利润最高？最高利润是多少？
如图，反比例函数
与正比例函数y=ax相交于A（1，k），B（-k，-1）两点。
（1）求反比例函数和正比例函数的解析式；
（2）将正比例函数y=ax的图象平移，得到一次函数y=ax+b的图象，与函数的图象交于C（x1，y1）、D（x2，y2），且|x1-x2|·|y1-y2|=5，求b的值。
某市自来水公司为限制单位用水，每月只给某单位计划内用水3000吨，计划内用水每吨收费0.5元，超计划部分每吨按0.8元收费．
（1）写出该单位水费y（元）与每月用水量x（吨）之间的函数关系式：
①用水量小于等于3000吨 ；
②用水量大于3000吨 ．
（2）某月该单位用水3200吨，水费是 元；若用水2800吨，水费 元．
（3）若某月该单位缴纳水费1540元，则该单位用水多少吨？
在一条笔直的公路上有A、B两地，甲骑自行车从A地到B地；乙骑自行车从B地到A第，到达A地后立即按原路返回，如图是甲、乙两人离B地的距离y（km）与行驶时间x（h）之间的函数图象，根据图象解答以下问题：
（1）A、B两地之间的距离： km；
（2）甲的速度为 km/h；乙的速度为30km/h；
（3）点M的坐标为 ；
（4）求：甲离B地的距离y（km）与行驶时间x（h）之间的函数关系式（不必写出自变量的取值范围）．
已知一次函数
（1）
为何值时，
随
的增大而减小？
（2）为何值时，它的图象经过原点？
小王从A地前往B地，到达后立刻返回．他与A地的距离y（千米）和所用时间x（小时）之间的函数关系如图所示．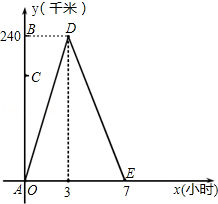
（1）小王从B地返回到A地用了多少小时？
（2）求小王出发6小时后距A地多远？
（3）在A、B之间有一C地，小王从去吋途经C地，到返回时路过C地，共用了2小时20分，求A、C 两地相距多远？
有一个附有进水管、出水管的水池，每单位时间内进出水管的进、出水量都是一定的，设从某时刻开始，4h内只进水不出水，在随后的时间内不进水只出水，得到的时间x（h）与水量y（m3）之间的关系图（如图）．回答下列问题：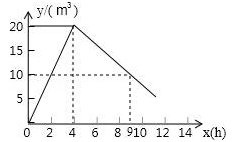
（1）进水管4h共进水多少？每小时进水多少？
（2）当0≤x≤4时，y与x有何关系？
（3）当x=9时，水池中的水量是多少？
（4）若4h后，只放水不进水，那么多少小时可将水池中的水放完？
-|m-1|．
，试判断直线
一定经过哪些象限，并说明理由。
粤公网安备 44130202000953号