四川省乐山市峨边彝族自治县九年级适应性考试数学试卷
下列说法错的是
A.不等式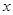 <2的正整数解只有一个 <2的正整数解只有一个 |
B.-2是不等式2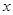 -1<0的一个解 -1<0的一个解 |
C.不等式-3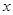 >9的解集是 >9的解集是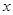 >-3 >-3 |
D.不等式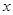 <10的整数解有无数个 <10的整数解有无数个 |
为了解峨边今年参加中考的1000名学生的体重情况,抽查了其中200名学生的体重进行统计分析,下列叙述正确的是:
| A.200名学生是总体 |
| B.200名学生的体重是总体的一个样本 |
| C.每名学生是总体的一个个体 |
| D.以上调查是普查 |
如图,球从A处射击,经过台边挡板CD反击,击中球B;已知AC=10cm,BD=15cm,CD=50cm,
则点E距点C的距离是
| A.20cm | B.30cm | C.15cm | D.35cm |
如图,AB为⊙O直径,弦CD⊥AB于点E,已知CD=12,BE=2,则⊙O的直径为:
| A.8 | B.10 | C.16 | D.20 |
如图:y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x<ax+4的解集为: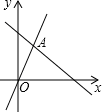
A.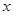 < <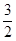 |
B.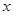 >3 >3 |
C.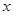 > >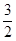 |
D.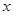 <3 <3 |
已知二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图象如图所示,有下列结论:①abc>0;②b2-4ac<0;③a-b+c>0;④4a-2b+c<0其中正确结论的个数是: 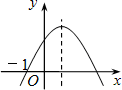
| A.1 | B.2 | C.3 | D.4 |
如图,把一个等边三角形纸片,剪掉一个角后,所得到一个四边形;则图形中∠1+∠2的度数是______.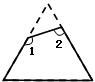
如图,正六边形ABCDEF的边长为2 cm,点P为六边形内任一点.则点P到各边距离之和为 .
cm,点P为六边形内任一点.则点P到各边距离之和为 .
如图:由三角形摆成的图案;摆第1层需一个三角形,摆第2层需要3个三角形;摆第3层需要7个三角形,摆第4层需要13个三角形,摆第5层需要 个三角形……摆到第n层需要____个三角形。
如图:在平行四边形ABCD中,点E在BA的延长线上,且:BE=AD,点F在AD上,AF=AB
求证:CF=EF
已知如图,在平面直角坐标系中,一次函数 =
=
 +b(
+b( ≠0)的图象与反比例函数
≠0)的图象与反比例函数 =
= (
( ≠0)的图象交于一、三象限内A、B两点,与
≠0)的图象交于一、三象限内A、B两点,与 轴交于点C;点A(2,m),点B(n,-2),且t
轴交于点C;点A(2,m),点B(n,-2),且t n∠Boc=
n∠Boc= ;
;
(1)求一次函数和反比例函数的解析式;
(2)在 轴上有一点E(O点除外),使得△BCE与△BCO的面积相等,求点E的坐标。
轴上有一点E(O点除外),使得△BCE与△BCO的面积相等,求点E的坐标。
某校初三学生去社会实践,在风景区看到一棵汉白杨树,好高哟,数学老师说请小明和小华同学用数学知识测量,全体同学计算这棵树多高,下面是这两位同学的对话。
小明:我站在此处看到树顶仰角45°;
小华:我站在此处看到树顶仰角30°
小明、小华身高都是1.6米,两人相距20米,请你来根据两位同学的对话,结合图形,算出这棵汉白杨的高(参考数据 ≈1.414
≈1.414  ≈1.732,结果保留三个有效字)。
≈1.732,结果保留三个有效字)。
某班数学科代表小红对本班上学期期末考试成绩(成绩取整数,满分100分)作了统计分析,绘制成如下 频数,频率统计表和频率分布直方图。请你根据图表中提供的信息解答下列问题,
(1)频数频率表中的a=____b=____;
(2)补全频数分布直方图;
(3)小红在班上任选一名同学,该同学数学成绩不低于80分的概率是多少?

已知如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC,过点C作⊙O的切线,交OD的延长线于点E,连接BE:
(1)求证:BE是⊙O的切线;
(2)连接AD并延长交BE于点F,若OB=9,Sin∠ABC= ,求BF的长。
,求BF的长。
关于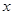 的一元二次方程
的一元二次方程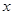 2+2
2+2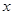 +
+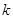 +1=O的实数解是
+1=O的实数解是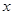 1和
1和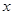 2;
2;
(1)求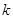 的取值范围;
的取值范围;
(2)如果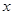 1+
1+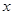 2-
2-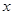 1
1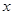 2<-1,且
2<-1,且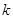 为整数,求
为整数,求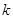 的值。
的值。
如图,点P是菱形ABCD的对角线BD上的一点,连接CP并延长 ,交AD于E,交BA的延长线于F。
(1)求证:∠DCP=∠DAP.
(2)若AB=2,DP:PB=1:2,且PA⊥BF,求对角线BD的长。
将一副直角三角板(Rt△ABC和Rt△DEF),按图1所示的方式摆放,∠ACB=90°,CA=CB,∠FDE=90°,O是AB中点,D与点O重合,DF⊥AC于点M,DE⊥BC于点N,试判断线段OM与ON的数量关系,并写出证明过程。
小宇同学展示出如下正确的解法:
解OM=ON,
证明:连OC,则OC是斜边AB上中线:
∵CA=CB,
∴OC是∠ACB的平分线(依据1);
∵OM⊥AC,ON⊥BC;
∴OM=ON(依据2)
(1)上述证明过程中的“依据1”“依据2”分别是指:依据1_____依据2______。
(2)你有与小宇不同的思考方法吗?请写出你的证明过程:
(3)将图(1)中的Rt△DEF沿着射线BA方向平移至图(2)所示的图形位置,使点D落在BA的延长线上,FD的延长线与CA的延长线垂直相交于点M,BC的延长线与DE垂直相交于N,连接OM、ON,试判断线段OM、ON的数量关系和位置关系,并写出证明过程。
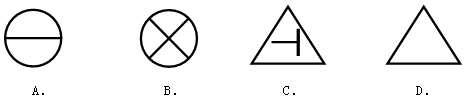
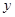 =
=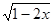 中,自变量
中,自变量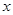 的取值范围是:
的取值范围是: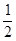

 、b在数轴上对应位置如图所示:化简:
、b在数轴上对应位置如图所示:化简: +∣
+∣
 =
= ,求代数式(
,求代数式( —
— )÷
)÷ 的值
的值 轴交于A(1,0),B(-3,0)两点,与
轴交于A(1,0),B(-3,0)两点,与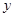 轴交于点C(0,3),抛物线顶点P,连接AC。
轴交于点C(0,3),抛物线顶点P,连接AC。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号