甲、乙两支清雪队同时开始清理某路段积雪，一段时间后，乙队被调往别处，甲队又用了3小时完成了剩余的清雪任务，已知甲队每小时的清雪量保持不变，乙队每小时清雪50吨，甲、乙两队在此路段的清雪总量y（吨）与清雪时间x（时）之间的函数图象如图所示．
（1）乙队调离时，甲、乙两队已完成的清雪总量为 吨；
（2）求此次任务的清雪总量
；
（3）求乙队调离后y与x之间的函数关系式．
已知一次函数
的图象与反比例函数
图象交于点 P（4，n）。求P点坐标
求一次函数的解析式
若点A（
，
），B（
，
）在上述一次函数的图象上，且
，试比较、 的大小，并说明理由。
在一条笔直的公路上有A、B两地，甲骑自行车从A地到B地；乙骑自行车从B地到A第，到达A地后立即按原路返回，如图是甲、乙两人离B地的距离y（km）与行驶时间x（h）之间的函数图象，根据图象解答以下问题：
（1）A、B两地之间的距离： km；
（2）甲的速度为 km/h；乙的速度为30km/h；
（3）点M的坐标为 ；
（4）求：甲离B地的距离y（km）与行驶时间x（h）之间的函数关系式（不必写出自变量的取值范围）．
某市自来水公司为限制单位用水，每月只给某单位计划内用水3000吨，计划内用水每吨收费0.5元，超计划部分每吨按0.8元收费．
（1）写出该单位水费y（元）与每月用水量x（吨）之间的函数关系式：
①用水量小于等于3000吨 ；
②用水量大于3000吨 ．
（2）某月该单位用水3200吨，水费是 元；若用水2800吨，水费 元．
（3）若某月该单位缴纳水费1540元，则该单位用水多少吨？
已知：y是x一次函数，且当
＝2时，
；且当＝—2时，y＝1试求
与之间的函数关系式并画出图象；在图象上标出与x轴、y轴的交点坐标
当
取何值时，＝5 ？
(10分)如图：一次函数y=－
x+6的图象与x轴和y轴分别交于点A和B ,再将△AOB
沿直线CD对折，使点A与点B重合。直线CD与x轴交于点C,与AB交于点D。
(1)点A的坐标为 ，点B的坐标为 。
(2)求OC的长度 ；
(3)在x轴上有一点P，且△PAB是等腰三角形,不需计算过程，请直接写出点P的坐标 。
已知一次函数
（1）
为何值时，
随
的增大而减小？
（2）为何值时，它的图象经过原点？
如图，已知点A、P在反比例函数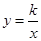
（
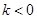）的图象上，点B、Q在直线
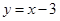的图象上，点B的纵坐标为﹣1，AB⊥x轴，且
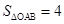，若P、Q两点关于y轴对称，设点P的坐标为（m，n）．
（1）求点A的坐标和k的值；
（2）求
的值．
已知函数y=kx+b的图象经过点A（- 3, - 2）及点B（1, 6）．
（1）求此一次函数解析式,并画图象； （2）求函数y=2x+4图象与坐标轴围成的三角形的面积．
如图，已知直线
：
与直线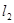
：y = mx－4m的图像的交点C 在第四象限，且点C到y轴的距离为2．
（1）求直线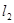的解析式；
（2）求△ADC的面积；
（3）在第一象限的角平分线上是否存在点P，使得△ADP的面积是△ADC的面积的2倍？如果存在，求出点P的坐标，如果不存在，请说明理由．
如图,长方形ABCD的边长分别为AB=12cm,AD=8cm,点P、Q都从点A出发，分别沿AB-CD运动，且保持AP=AQ，在这个变化过程中，图中的阴影部分的面积也随之变化。
当AP由2cm变到8cm时，图中阴影部分的面积是增加了，还是减少了？增加或减少了多少平方厘米？
小王从A地前往B地，到达后立刻返回．他与A地的距离y（千米）和所用时间x（小时）之间的函数关系如图所示．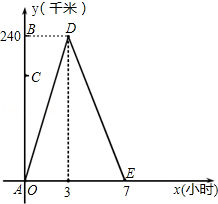
（1）小王从B地返回到A地用了多少小时？
（2）求小王出发6小时后距A地多远？
（3）在A、B之间有一C地，小王从去吋途经C地，到返回时路过C地，共用了2小时20分，求A、C 两地相距多远？
如图，一次函数y=kx+b（k≠0）的图象过点P（﹣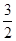
，0），且与反比例函数
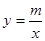（m≠0）的图象相交于点A（﹣2，1）和点B．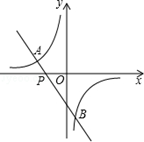
（1）求一次函数和反比例函数的解析式；
（2）求点B的坐标，并根据图象回答：当x在什么范围内取值时，一次函数的函数值小于反比例函数的函数值？
某动车站在原有的普通售票窗口外新增了无人售票窗口，普通售票窗口从上午8点开放，而无人售票窗口从上午7点开放，某日从上午7点到10点，每个普通售票窗口售出的车票数
（张）与售票时间x（小时）的变化趋势如图1，每个无人售票窗口售出的车票数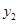
（张）与售票时间x（小时）的变化趋势是以原点为顶点的抛物线的一部分，如图2，若该日截至上午9点，每个普通售票窗口与每个无人售票窗口售出的车票数恰好相同．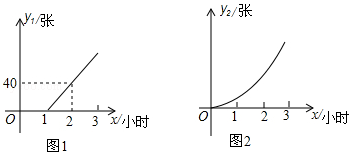
（1）求图2中所确定抛物线的解析式；
（2）若该日共开放5个无人售票窗口，截至上午10点，两种窗口共售出的车票数不少于900张，则至少需要开放多少个普通售票窗口？
粤公网安备 44130202000953号