江苏省兴化顾庄等三校八年级上学期期末考试数学试卷
以下问题,不适合用全面调查的是( )
| A.了解全班同学每周体育锻炼的时间 | B.某书中的印刷错误 |
| C.了解一批电视机的使用寿命 | D.旅客上飞机前的安检 |
在3.14、 、
、 这3个数中,无理数有( )
这3个数中,无理数有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
如果点P(m ,1-2m)在第一象限,那么m的取值范围是( )
A.0<m< |
B.- <m<0 <m<0 |
C.m<0 | D.m> |
若坐标系中某图形上所有点的横坐标、纵坐标都变为原来的相反数,图形的大小、形状和位置不变,则这个图形不可能是( )
| A.平行四边形 | B.圆 | C.线段 | D.等边三角形 |
已知点(-1,y1),(2,y2)都在直线y = x+2上,则y1与 y2大小关系是 .
在边长为16cm的正方形铁皮上剪去一个圆,则剩下的铁皮的面积S(cm2)与圆的半径r(cm)之间的函数表达式为 (不要求写自变量的取值范围).
已知平行四边形ABCD中,∠ABC的平分线交AD于点E,且AE=2,DE=1,则平行四边形ABCD的周长等于 .
如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.当△ABC满足条件 时,四边形DBFE是菱形.
如图,已知矩形ABCD,AB在y轴上,AB=2,BC=3,点A的坐标为(0,1),在AD边上有一点E(1,1),过点E的直线平分矩形ABCD的面积,则此直线的解析式为 .
(本题满分10分) 如图,在△ABC中,已知AB=AC=5,AD平分∠BAC,E是AC边的中点.
(1)求DE的长;
(2)若AD的长为4,求△DEC的面积.
(本题满分10分)已知:如图,平行四边形ABCD中,AB⊥AC,对角线AC、BD交于O点,将直线AC绕点O顺时针旋转,分别交BC、AD于点E、F.
(1) 当旋转角为90°时,求证:四边形ABEF是平行四边形;
(2) 求证:在旋转过程中,AF=EC.
(本题满分10分) 如图,已知6×6的正方形网格中,每一个小正方形的边长为1,△ABC的顶点A、B、C都在小正方形的顶点上.

|
(2)在方格纸上画出一个格点三角形,使其与△ABC全等且有一个公共顶点B;
(3)画
 ,使它与△ABC关于直线l对称.
,使它与△ABC关于直线l对称.(本题满分10分) 在我市开展的“增强学生体质,丰富学校生活”活动中,某校根据实际情况,决定主要开设A:乒乓球,B:篮球,C:跑步,D:跳绳这四种运动项目.为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图和扇形统计图.请你结合图中的信息解答下列问题:
(1)样本中喜欢B项目的人数百分比是 ,其所在扇形统计图中的圆心角的度数是
(2)把条形统计图补充完整;
(3)已知该校有750人,估计全校喜欢乒乓球的人数是多少?
已知四边形ABCD是矩形,对角线AC和BD相交于点P,若在矩形的上方加一个△DEA,且使DE∥AC,AE∥BD.
(1)求证:四边形DEAP是菱形;
(2)若AE=CD,求∠DPC的度数.
如图,公路上有A、B、C三个汽车站,一辆汽车8︰00从离A站10km的P地出发,向C站匀速行驶,15min后离A站30km.
(1)设出发x h后,汽车离A站y km,写出y与x之间的函数表达式;
(2)当汽车行驶到离A站250km的B站时,接到通知要在12︰00前赶到离B站60km的C站.汽车按原速行驶,能否准时到达?如果能,那么汽车何时到达C站?
如图,已知直线 :
: 与直线
与直线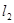 :y = mx-4m的图像的交点C 在第四象限,且点C到y轴的距离为2.
:y = mx-4m的图像的交点C 在第四象限,且点C到y轴的距离为2.
(1)求直线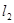 的解析式;
的解析式;
(2)求△ADC的面积;
(3)在第一象限的角平分线上是否存在点P,使得△ADP的面积是△ADC的面积的2倍?如果存在,求出点P的坐标,如果不存在,请说明理由.





 ,则底角为 .
,则底角为 . )与点Q ( b,2)关于y轴对称, 则a + b= .
)与点Q ( b,2)关于y轴对称, 则a + b= . ; (2)
; (2) .
. ; (2) 8(x-1)3=27.
; (2) 8(x-1)3=27.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号