如图,一次函数y=kx+3的图象分别交x轴、y轴于点C、点D,与反比例函数 的图象在第四象限相交于点P,并且PA⊥x轴于点A,PB⊥y轴于点B,已知B(0,-6)且S△DBP=27.
的图象在第四象限相交于点P,并且PA⊥x轴于点A,PB⊥y轴于点B,已知B(0,-6)且S△DBP=27.
(1)求上述一次函数与反比例函数的表达式;
(2)设点Q是一次函数y=kx+3图象上的一点,且满足△DOQ的面积是△COD面积的2倍,直接写出点Q的坐标.
(3)若反比例函数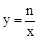 的图象与△ABP总有公共点,直接写出n的取值范围.
的图象与△ABP总有公共点,直接写出n的取值范围.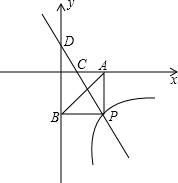
如图,已知一次函数y =-x+7与正比例函数y= x的图象交于点A,且与x轴交于点B.
x的图象交于点A,且与x轴交于点B.
(1)求点A和点B的坐标;
(2)过点A作AC⊥y轴于点C,过点B作直线l∥y轴.动点P从点O出发,以每秒1个单位长的速度,沿O—C—A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒.
①当t为何值时,以A、P、R为顶点的三角形的面积为8?
②是否存在以A、P、Q为顶点的三角形是直角三角形?若存在,求t的值;若不存在,请说明理由.
如图,直线AC是一次函数y=2x+3的图象,直线BC是一次函数y=﹣2x﹣1的图象.
(1)求A、B、C三点的坐标;
(2)求△ABC的面积.
如图①,在平行四边形ABCD中,AB=13,BC=50,BC边上的高为12.点P从点B出发,沿B﹣A﹣D﹣A运动,沿B﹣A运动时的速度为每秒13个单位长度,沿A﹣D﹣A运动时的速度为每秒8个单位长度.点Q从点B出发沿BC方向运动,速度为每秒5个单位长度.P、Q两点同时出发,当点Q到达点C时,P、Q两点同时停止运动.设点P的运动时间为t(秒).连结PQ.
(1)当点P沿A﹣D﹣A运动时,求AP的长(用含t的代数式表示).
(2)连结AQ,在点P沿B﹣A﹣D运动过程中,当点P与点B、点A不重合时,记△APQ的面积为S.求S与t之间的函数关系式.
(3)过点Q作QR∥AB,交AD于点R,连结BR,如图②.在点P沿B﹣A﹣D运动过程中,当线段PQ扫过的图形(阴影部分)被线段BR分成面积相等的两部分时t的值.
(4)设点C、D关于直线PQ的对称点分别为C′、D′,直接写出C′D′∥BC时t的值.
学习“一次函数”时,我们从“数”和“形”两方面研究一次函数的性质,并积累了一些经验和方法,尝试用你积累的经验和方法解决下面问题.
(1)在平面直角坐标系中,画出函数y=|x|的图象:
①列表:完成表格
| x |
… |
﹣3 |
﹣2 |
﹣1 |
0 |
1 |
2 |
3 |
… |
| y |
… |
|
|
|
|
|
|
|
|
②画出y=|x|的图象;
(2)结合所画函数图象,写出y=|x|两条不同类型的性质;
(3)直接写出函数y=|x﹣2|图象是由函数y=|x|图象怎样平移得到?

如图,A(1,0),B(4,0),M(5,3).动点P从点A出发,沿x轴以每秒1个单位长的速度向右移动,且过点P的直线l:y=-x+b也随之移动.设移动时间为t秒.
(1)当t=1时,求l的解析式;
(2)若l与线段BM有公共点,确定t的取值范围;
(3)直接写出t为何值时,点M关于l的对称点落在y轴上.如不存在,请说明理由.
如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3 ).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的面四民﹒数学兴趣小组对捐款情况进行了抽样调查,速度分别为1,
).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的面四民﹒数学兴趣小组对捐款情况进行了抽样调查,速度分别为1, ,2 (长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以
,2 (长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以 (长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
(长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
请解答下列问题:
(1)过A,B两点的直线解析式是 ;
(2)当t﹦4时,点P的坐标为 ;当t ﹦ ,点P与点E重合;
(3)① 作点P关于直线EF的对称点P′.在运动过程中,若形成的四边形PEP′F为菱形,则t的值是多少?② 当t﹦2时,是否存在着点Q,使得△FEQ ∽△BEP ?若存在, 求出点Q的坐标;若不存在,请说明理由.
如图,直线y=- x+6分别与x轴、y轴交于A、B两点;直线y=
x+6分别与x轴、y轴交于A、B两点;直线y= x与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿
x与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿 轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN,设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).
轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN,设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).
(1)求点C的坐标;
(2)当0<t<5时,求S与t之间的函数关系式,并求S的最大值;
(3)当t>0时,直接写出点(4, )在正方形PQMN内部时t的取值范围.
)在正方形PQMN内部时t的取值范围.
如图,梯形ABCD中,AB∥CD,AB=14,AD= 4 ,CD=7.直线l经过A,D两点,且sin∠DAB=
,CD=7.直线l经过A,D两点,且sin∠DAB= .动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于AB,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
.动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于AB,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
(1)求腰BC的长;
(2)当Q在BC上运动时,求S与t的函数关系式;
(3)在(2)的条件下,是否存在某一时刻t,使得△MPQ的面积S是梯形ABCD面积的 ?若存在,请求出t的值;若不存在,请说明理由;
?若存在,请求出t的值;若不存在,请说明理由;
(4)随着P,Q两点的运动,当点M在线段DC上运动时,设PM的延长线与直线l相交于点N,试探究:当t为何值时,△QMN为等腰三角形?
已知:如图,直线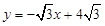 与x轴相交于点A,与直线
与x轴相交于点A,与直线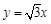 相交于点P(2,
相交于点P(2,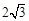 ).
).
(1)请判断 的形状并说明理由.
的形状并说明理由.
(2)动点E从原点O出发,以每秒1个单位的速度沿着O→P→A的路线向点A匀速运动(E不与点O、A重合),过点E分别作EF⊥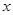 轴于F,EB⊥
轴于F,EB⊥ 轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.
轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.
求:① S与t之间的函数关系式.
② 当t为何值时,S最大,并求S的最大值
如图①,一条笔直的公路上有A、B、C三地,B、C两地相距150千米,甲、乙两辆汽车分别从B、C两地同时出发,沿公路匀速相向而行,分别驶往C、B两地.甲、乙两车到A地的距离y1、y2(千米)与行驶时间x(时)的关系如图②所示.根据图象进行以下探究:

(1)请在图①中标出A地的位置,并作简要的文字说明;
(2)求图②中M点的坐标,并解释该点的实际意义;
(3)在图②中补全甲车的函数图象,求甲车到A地的距离y1与行驶时间x的函数关系式;
(4)A地设有指挥中心,指挥中心及两车都配有对讲机,两部对讲机在15千米之内(含15千米)时能够互相通话,求两车可以同时与指挥中心用对讲机通话的时间.
如图,在直角坐标系xOy中,直线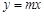 与双曲线
与双曲线 相交于
相交于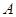 、B
、B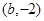 两点,矩形
两点,矩形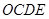 的边
的边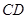 恰好被点
恰好被点 平分,边
平分,边 交双曲线于
交双曲线于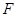 点,四边形
点,四边形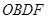 的面积为2.
的面积为2.
(1)求n的值;
(2)求不等式 的解集
的解集
在平面直角坐标系xOy中,直线 分别与x轴,y轴交于过点A,B,点C是第一象限内的一点,且AB=AC,AB⊥AC,抛物线
分别与x轴,y轴交于过点A,B,点C是第一象限内的一点,且AB=AC,AB⊥AC,抛物线 经过A,C两点,与
经过A,C两点,与 轴的另一交点为D.
轴的另一交点为D.
(1)求此抛物线的解析式;
(2)判断直线AB与CD的位置关系,并证明你的结论;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,B,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
某地区冬季干旱,康平社区每天需从外地调运饮用水60吨.有关部门紧急部署,从甲、乙两水厂调运饮用水到供水点,甲厂每天最多可调出40吨,乙厂每天最多可调出45吨.从两水厂运水到康平社区供水点的路程和运费如下表:
| |
到康平社区供水点的路程(千米) |
运费(元/吨·千米) |
| 甲厂 |
20 |
4 |
| 乙厂 |
14 |
5 |
(1)若某天调运水的总运费为4450元,则从甲、乙两水厂各调运了多少吨饮用水?
(2)设从甲厂调运饮用水x吨,总运费为W元,试写出W关于x的函数关系式,并确定x的取值范围.怎样安排调运方案才能使每天的总运费最省?
如图,直线y=-2x+8交x轴于A,交y轴于B i点p在线段AB上,过点P分别向x轴、y轴引垂线,垂足为C、D,设点P的横坐标为m,矩形PCOD的面积为S.
(1)求S与m的函数关系式; (2)当m取何值时矩形PCOD的面积最大,最大值是多少.