（本题12分）如图1，已知在直角坐标系XOY中，正△OBC的边长和等腰直角△DEF的底边都为6，点E与坐标原点O重合，点D、B在X轴上，连结FC，在△DEF沿X轴的正方向以每秒
个单位运动时，边EF所在直线和边OC所在直线相交于G，设运动时间为t.
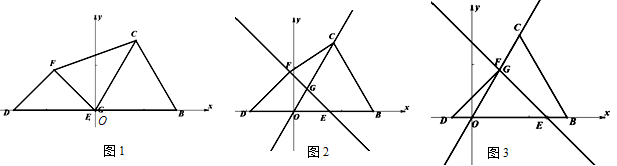
（1）如图2，当t=1时，①求OE的长；②求∠FGC的度数；③求G点坐标；
（2）①如图3，当t为多少时，点F恰在△OBC的OC边上；
②在点F、C、G三点不共线时，记△FCG的面积为S，用含t的代数式表示S，并写出t的相应取值范围.
相关试题
，并把解集在数轴上表示出来．
，其中
．某工厂有一种材料，可加工甲、乙、丙三种型号机械配件共240件，厂方计划由20个工人一天内加工完成，并要求每人只加工一种配件，根据下表提供的信息，解答下列问题：
| 配件种类 |
甲 |
乙 |
丙 |
| 每人可加工配件的数量（个） |
16 |
12 |
10 |
| 每个配件获利（元） |
6 |
8 |
5 |
（1）设加工甲种配件的人数为x，加工乙种配件的人数为y，求y与x之间的函数关系式
（2）如果加工每种配件的人数均不少于3人，那么加工配件的人数安排方案有几种？并写出每种安排方案
（3）要使此次加工配件的利润最大，应采用哪种方案？最大利润是多少？
相关知识点
推荐套卷
粤公网安备 44130202000953号