初中数学一次函数的最值解答题

如图，已知反比例函数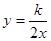和一次函数y=2x-1，其中一次函数的图象经过（a，b），（a+1，b+k）两点．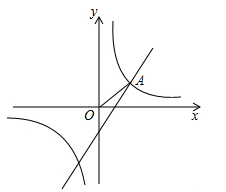

（1）求反比例函数的解析式；
（2）如图，已知点A在第一象限，且同时在上述两个函数的图象上，求点A的坐标；
（3）利用（2）的结果，请问：在x轴上是否存在点P，使△AOP为等腰三角形？若存在，把符合条件的P点坐标都求出来；若不存在，请说明理由．

某市出租车的收费标准为：不超过3km的计费为7．0元，3km后按2．4元/km计费．
（1）当行驶路程x超过3km时，写出车费y（元）与行驶路程x（km）之间的函数关系式；
（2）若小明乘出租车的行驶路程为5km，则小明应付车费多少元？
（3）若小亮乘出租车出行，付费19元，则小亮乘车的路程为多少km？

杨佳明周日骑车从家里出发，去图书馆看书，
（1）若杨佳明骑车行驶的路程y（km）与时间t（min）的图象如图1所示，请说出线段AB所表示的实际意义：          ；若杨佳明在第30分钟时以来时的速度原路返回，请在图上补出她返回时行驶的路程y（km）与时间t（min）的图象；
（2）在整个骑行过程中，若杨佳明离家的距离y（km）与时间t（min）的图象如图2所示，请说出线段AB所表示的实际意义：           ；若杨佳明在第30分钟时以来时的速度原路返回，请在图上补出她返回时离家的距离y（km）与时间t（min）的图象；
（3）在整个骑行过程中，若杨佳明骑车的速度y（km/min）与时间t（min）的图象如图3所示，那么当她离家最远时，时间是在第     分钟，并求出她在骑行30分钟时的路程是        ．

已知y=y₁+y₂，y₁与x成正比例，y₂与x-1成正比例，并且当x=2时，y=6；当x=3时，y=5，求y与x的函数关系式．

函数y=ax+b，当x=1时，y=1；当x=2时，y=-5．
（1）求a，b的值．
（2）当x=0时，求函数值y．
（3）当x取何值时，函数值y为0．

某商场以每件20元的价格购进一种商品，试销中发现，这种商品每天的销售量m（件）与每件的销售价x（元）满足关系：m=140-2x．
（1）写出商场卖这种商品每天的销售利润y与每件的销售价x间的函数关系式；
（2）如果商场要想每天获得最大的销售利润，每件商品的售价定为多少最合适？最大销售利润为多少？

某商场购进一种单价为元的篮球，如果以单价元售出，那么每天可售出50个．根据销售经验，售价每提高元．销售量相应减少1个。
（1）假设销售单价提高元，那么销售每个篮球所获得的利润是_____元；这种篮球每天的销售量是_________个。
（2）假设每天销售这种篮球所得利润为y ,请用含的代数式表示y。
（3）假如你是商场老板，为了在出售这种篮球时获得最大利润，你该提高多少元？最大利润是多少？请说明理由。

大润发超市进了一批成本为8元/个的文具盒。调查发现: 这种文具盒每个星期的销售量个）与它的定价（元/个）的关系如图所示：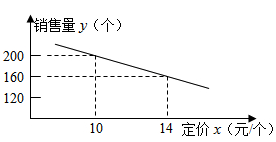

（1）求这种文具盒每个星期的销售量个）与它的定价（元/个）之间的函数关系式（不必写出自变量的取值范围）
（2）每个文具盒定价是多少元时，超市每星期销售这种文具盒（不考虑其他因素）可获得的利润最高？最高利润是多少?

如图，直线y = kx+6与x轴y轴分别相交于点E，F。点E的坐标为（- 8，0），点A的坐标为（- 6，0）。 点P（x，y）是第二象限内的直线上的一个动点。

（1）求k的值；
（2）当点P运动过程中，试写出△OPA的面积S与x的函数关系式，并写出自变量x的取值范围；
（3）探究：当P运动到什么位置（求P的坐标）时，△OPA的面积为，并说明理由

甲、乙两组工人同时加工某种零件，乙组工作中有一次停产更换设备，更换
设备后，乙组的工作效率是原来的2倍．两组各自加工零件的数量（件）与时间（时）的函数图象如图所示．

（1）求甲组加工零件的数量y与时间之间的函数关系式．
（2）当x=2．8时，甲、乙两组共加工零件          件；乙组加工零件总量的值为          ．
（3）加工的零件数达到230件装一箱，零件装箱的时间忽略不计，若甲、乙两组加工出的零件合在一起装箱，当甲组工作多长时间恰好装满第2箱？

如图所示，直线与x轴、y轴分别交于点A和点B，M是OB上的一点，若将△ABM沿AM折叠，点B恰好落在x轴上的点B′处

求（1）点B′、M的坐标
（2）直线AM的解析式。

已知一次函数的图象过点A（3，0），B（—1，2），

（1）求直线AB的解析式；
（2）在给出的直角坐标系中，画出和的图象，并根据图象写出方程组的解．

如图，已知点是一次函数图象与反比例函数图象的一个交点．
（1）求一次函数的解析式；
（2）在y轴的右侧，当时，直接写出的取值范围．

某商店试销一款运动服，经市场调查，发现平均日销量y（件）是销售单价x（元/件）的一次函数，其图象如图所示．

（1）根据图象，求y与x之间的函数表达式；
（2）当销售单价为多少元时，平均日销售量是150件？

如图1，直线l₁：y=x+1与l₂：y=﹣2x+6相交于点C，直线l₁分别与x轴、y轴相交于点A、D，直线l₂分别与x轴、y轴交于点B、E．

（1）填空：①线段AB=      ；②点C的坐标为       ；
（2）求证：△ABC是直角三角形；
（3）直线l₁向上平移几个单位后，以点A、B、E、D为顶点的图形是轴对称图形？（直接写出答案）