初中数学一次函数的最值计算题

小王从A地前往B地，到达后立刻返回．他与A地的距离y（千米）和所用时间x（小时）之间的函数关系如图所示．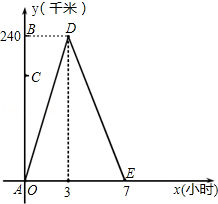

（1）小王从B地返回到A地用了多少小时？
（2）求小王出发6小时后距A地多远？
（3）在A、B之间有一C地，小王从去吋途经C地，到返回时路过C地，共用了2小时20分，求A、C 两地相距多远？

有一个附有进水管、出水管的水池，每单位时间内进出水管的进、出水量都是一定的，设从某时刻开始，4h内只进水不出水，在随后的时间内不进水只出水，得到的时间x（h）与水量y（m³）之间的关系图（如图）．回答下列问题：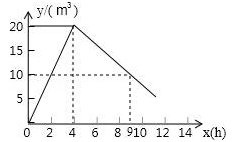

（1）进水管4h共进水多少？每小时进水多少？
（2）当0≤x≤4时，y与x有何关系？
（3）当x=9时，水池中的水量是多少？
（4）若4h后，只放水不进水，那么多少小时可将水池中的水放完？

已知函数y=2x+b的图像经过点（a，7）和（-2，a），求这个函数的表达式．

某市自来水公司为限制单位用水，每月只给某单位计划内用水3000吨，计划内用水每吨收费0.5元，超计划部分每吨按0.8元收费．
（1）写出该单位水费y（元）与每月用水量x（吨）之间的函数关系式：
①用水量小于等于3000吨      ；
②用水量大于3000吨      ．
（2）某月该单位用水3200吨，水费是      元；若用水2800吨，水费      元．
（3）若某月该单位缴纳水费1540元，则该单位用水多少吨？

如图，函数的图象与函数（）的图象交于A（，1）B（1，）两点．

（1）求函数的表达式；    
（2）观察图象，比较当时，与的大小．

如图，一次函数y=kx+b（k≠0）的图象过点P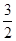（﹣，0），且与反比例函数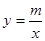（m≠0）的图象相交于点A（﹣2，1）和点B．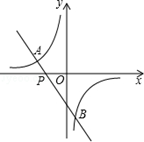

（1）求一次函数和反比例函数的解析式；
（2）求点B的坐标，并根据图象回答：当x在什么范围内取值时，一次函数的函数值小于反比例函数的函数值？

写出同时具备下列两个条件的一次函数关系式      ．（写出一个即可）
（1）y随x的增大而减小；
（2）图象经过点（1，﹣2）．

在一条笔直的公路上有A、B两地，甲骑自行车从A地到B地；乙骑自行车从B地到A第，到达A地后立即按原路返回，如图是甲、乙两人离B地的距离y（km）与行驶时间x（h）之间的函数图象，根据图象解答以下问题：

（1）A、B两地之间的距离：             km；
（2）甲的速度为          km/h；乙的速度为30km/h；
（3）点M的坐标为               ；
（4）求：甲离B地的距离y（km）与行驶时间x（h）之间的函数关系式（不必写出自变量的取值范围）．

已知一次函数
（1）为何值时，随的增大而减小？
（2）为何值时，它的图象经过原点？

（本小题满分10分）某班组织学生到百万葵园进行户外学习活动，已知百万葵园的门票销售分两类：一类为散客门票，票价每张120元；另一类为团体门票（一次性购买门票20张以上），每张门票价格在散客门票价格基础上打8折，设本次活动共有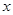人参加，购买门票需要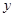元．
如果都买散客票，求y与x之间的函数关系式；
如果买团体票，求y与x之间的函数关系式，并写出自变量的取值范围；
请根据人数变化设计一种比较省钱的购票方案．

小文家与学校相距1000米．某天小文上学时忘了带一本书，走了一段时间才想起，于是返回家拿书，然后加快速度赶到学校．下图是小文与家的距离y（米）关于时间x（分钟）的函数图象．请你根据图象中给出的信息，解答下列问题：

（1）小文走了多远才返回家拿书？
（2）求线段AB所在直线的函数解析式；
（3）当x=8分钟时，求小文与家的距离．

如图，正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A（m，2），一次函数图象经过点B（-2，-1），与y轴的交点为C，与x轴的交点为D．

（1）求一次函数解析式；
（2）求C点的坐标；
（3）求△AOD的面积．

如图，已知点A、P在反比例函数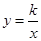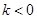（）的图象上，点B、Q在直线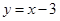的图象上，点B的纵坐标为﹣1，AB⊥x轴，且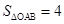，若P、Q两点关于y轴对称，设点P的坐标为（m，n）．

（1）求点A的坐标和k的值；
（2）求的值．

某动车站在原有的普通售票窗口外新增了无人售票窗口，普通售票窗口从上午8点开放，而无人售票窗口从上午7点开放，某日从上午7点到10点，每个普通售票窗口售出的车票数（张）与售票时间x（小时）的变化趋势如图1，每个无人售票窗口售出的车票数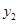（张）与售票时间x（小时）的变化趋势是以原点为顶点的抛物线的一部分，如图2，若该日截至上午9点，每个普通售票窗口与每个无人售票窗口售出的车票数恰好相同．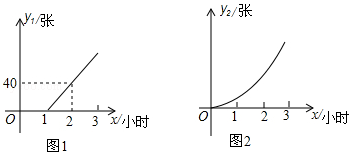

（1）求图2中所确定抛物线的解析式；
（2）若该日共开放5个无人售票窗口，截至上午10点，两种窗口共售出的车票数不少于900张，则至少需要开放多少个普通售票窗口？

经统计分析．某市跨河大桥上的车流速度v（千米／时）是车流密度x（辆／千米）的函数，当桥上的车流密度达到220辆／千米的时候就造成交通堵塞．此时车流速度为0千米／时；当车流密度不超过20辆／千米，车流速度为80千米／时．研究表明：当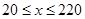时，车流速度v是车流密度x的一次函数．
（1）求大桥上车流密度为100辆／千米时的车流速度；
（2）在某一交通时段．为使大桥上的车流速度大于60千米／时且小于80千米／时，应把大桥上的车流密度控制在什么范围内？