雅美服装厂现有 种布料
种布料 ,
, 种布料
种布料 ,现计划用这两种布料生产
,现计划用这两种布料生产  、
、 两种型号的时装共
两种型号的时装共 套。已知做一套
套。已知做一套 型号的时装需用
型号的时装需用 种布料
种布料 ,
, 种布料
种布料 ,可获利润
,可获利润 元;做一套
元;做一套 型号的时装需用
型号的时装需用 种布料
种布料 ,
, 种布料
种布料 ,可获利润
,可获利润 元。若设生产
元。若设生产 型号的时装套数为
型号的时装套数为 ,用这批布料生产这两种型号的时装所获得的总利润为
,用这批布料生产这两种型号的时装所获得的总利润为 元。
元。
(1)请帮雅美服装厂设计出生产方案;
(2)求 (元)与
(元)与 (套)的函数关系,利用一次函数性质,选出(1)中哪个方案所获利润最大?最大利润是多少?
(套)的函数关系,利用一次函数性质,选出(1)中哪个方案所获利润最大?最大利润是多少?
已知一次函数 的图象与反比例函数
的图象与反比例函数 图象交于点 P(4,n)。
图象交于点 P(4,n)。求P点坐标
求一次函数的解析式
若点A(
 ,
, ),B(
),B( ,
, )在上述一次函数的图象上,且
)在上述一次函数的图象上,且 ,试比较
,试比较 、
、 的大小,并说明理由。
的大小,并说明理由。
已知:y是x一次函数,且当 =2时,
=2时, ;且当
;且当 =—2时,y=1
=—2时,y=1试求
 与
与 之间的函数关系式并画出图象;
之间的函数关系式并画出图象;在图象上标出与x轴、y轴的交点坐标
当
 取何值时,
取何值时, =5 ?
=5 ?
已知直线 与
与 轴交于点A(-4,0),与
轴交于点A(-4,0),与 轴交于点B.
轴交于点B.
求b的值
把△AOB绕原点O顺时针旋转90°后,点A落在
 轴的
轴的 处,点B若在
处,点B若在 轴的
轴的 处;
处;
①求直线 的函数关系式;
的函数关系式;
②设直线AB与直线 交于点C,矩形PQMN是△
交于点C,矩形PQMN是△ 的内接矩形,其中点P,Q在线段
的内接矩形,其中点P,Q在线段 上,点M在线段
上,点M在线段 上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.
上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.
如图,长方形ABCD的边长分别为AB=12cm,AD=8cm,点P、Q都从点A出发,分别沿AB-CD运动,且保持AP=AQ,在这个变化过程中,图中的阴影部分的面积也随之变化。 当AP由2cm变到8cm时,图中阴影部分的面积是增加了,还是减少了?增加或减少了多少平方厘米?
当AP由2cm变到8cm时,图中阴影部分的面积是增加了,还是减少了?增加或减少了多少平方厘米?
(本小题满分10分)
某商场试销一种成本为每件60元的服装,经试销发现,销售量 (件)与销售单价
(件)与销售单价 (元)符合一次函数
(元)符合一次函数 ,且
,且 时,
时, ;
; 时,
时, .
.
(1)求一次函数 的表达式;
的表达式;
(2)若该商场获得利润为 元,试写出利润
元,试写出利润 与销售单价
与销售单价 之间的关系式;
之间的关系式;
(3)若该商场想获得500元的利润且尽可能地扩大销售量,则销售单价应定为多少元?
(4)销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
.依法纳税是每个公民应尽的义务.从2008年3月1日起,新修改后的《中华人民共和国个人所得税法》规定,公民每月收入不超过2000元,不需交税;超过2000元的部分为全月应纳税所得额,都应纳税,且根据超过部分的多少按不同的税率纳税,详细的税率如下表:
| 级别 |
全月应纳税所得额 |
税率(%) |
| 1 |
不超过500元的部分 |
5 |
| 2 |
超过500元至2 000元的部分 |
10 |
| 3 |
超过2 000元至5 000元的部分 |
15 |
| 4 |
超过5 000元至20 000元的部分 |
20 |
| … |
… |
… |
(1)某工厂一名工人2008年3月的收入为2 400元,问他应交税款多少元?
(2)设x表示公民每月收入(单位:元),y表示应交税款(单位:元),
当2500≤x≤4000时,请写出y关于x的函数关系式;
(3)某公司一名职员2008年4月应交税款120元,问该月他的收入是多少元?
大学生李某投资在沙坪坝学校密集的沙南街路段投资开办了一个学生文具店.该店在开学前8月31日采购进一种今年新上市的文具袋.9月份(9月1日至9月30日)进行30天的试销售,购进价格为20
元/个.销售结束后,得知日销售量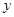 (个)与销售时间
(个)与销售时间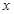 (天)之间有如下关系:
(天)之间有如下关系: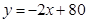 (
(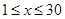 ,且
,且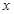 为整数);又知销售价格
为整数);又知销售价格 (元/个)与销售时间
(元/个)与销售时间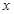 (天)之间的函数关系满足如图所示的函数图像.
(天)之间的函数关系满足如图所示的函数图像.
(1)求 关于
关于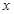 的函数关系式;
的函数关系式;
(2)求出在这30天(9月1日至9月30日)的试销中,日销售利润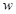 (元)与销售时间
(元)与销售时间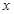 (天)之间的函数关系式;
(天)之间的函数关系式;
(3)“十一”黄金周期间,李某采用降低售价从而提高日销售量的销售策略.10月1日全天,销售价格比9月30日的销售价格降低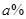 而日销售量就比9月30日提高了
而日销售量就比9月30日提高了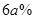 (其中
(其中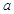 为小于15 的正整数),日销售利润比9月份最大日销售利润少569元,求
为小于15 的正整数),日销售利润比9月份最大日销售利润少569元,求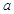 的值.
的值.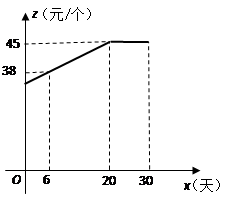 (参考数据:
(参考数据: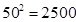 ,
,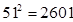 ,
,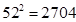 )
)