初中数学一次函数的最值计算题

如图①，已知直线y=-2x+4与x轴、y轴分别交于点A、C，以OA、OC为边在第一象限内作长方形OABC．

（1）求点A、C的坐标；
（2）将△ABC对折，使得点A的与点C重合，折痕交AB于点D，求直线CD的解析式（图②）；
（3）在坐标平面内，是否存在点P（除点B外），使得△APC与△ABC全等？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．

（本小题满分12分）如图，在直角坐标系xOy中，一次函数（m为常数）的图像与x轴交于A（-3，0），与y轴交于点C；以直线为对称轴的抛物线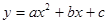（a，b，c为常数，且a＞0）经过A，C两点，与x轴正半轴交于点B．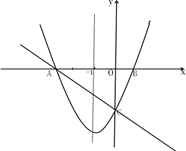

（1）求一次函数及抛物线的函数表达式。
（2）在对称轴上是否存在一点P，使得PBC的周长最小，若存在，请求出点P的坐标．
（3）点D是线段OC上的一个动点（不与点O、点C重合），过点D作DE‖PC交x轴于点E，连接PD、PE。设CD的长为m， PDE的面积为S。求S与m之间的函数关系式。并说明S是否存在最大值，若存在，请求出最大值：若不存在，请说明理由。

甲、乙两辆摩托车同时从相距20km的A、B两地出发，相向而行，图中分别表示甲、乙两辆摩托车到A地的距离s（km）与行驶时间t（h）的函数关系，则下列说法错误的是（   ）．

A．乙摩托车的速度较快
B．经过0．3小时甲摩托车行驶到A、B两地的中点
C．经过0．25小时两摩托车相遇
D．当乙摩托车到达A地时，甲摩托车距离A地km．

某商场购进一批单价为4元的日用品．若按每件5元的价格销售，每月能卖出3万件；若按每件6元的价格销售，每月能卖出2万件，假定每月销售件数y（件）与价格x（元/件）之间满足一次函数关系．
（1）试求y与x之间的函数关系式；
（2）当销售价格定为多少时，才能使每月的利润最大？每月的最大利润是多少？

如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，顶点A，C分别在坐标轴上，顶点B的坐标为（4，2），过点D（0，3）和E（6，0）的直线分别与AB，BC交于点M，N。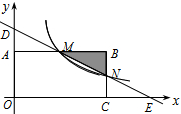

（1）求直线DE的解析式和点M的坐标；
（2）若反比例函数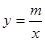（x>0）的图象经过点M，求该反比例函数的解析式，并通过计算判断点N是否在该函数的图象上；
（3）若反比例函数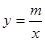（x>0）的图象与△MNB有公共点，请直接写出m的取值范围。

某冰箱厂为响应国家“家电下乡”号召，计划生产、两种型号的冰箱100台．经预算，两种冰箱全部售出后，可获得利润不低于 4.75万元，不高于4.8万元，两种型号的冰箱生产成本和售价如下表：

型号	A型	B型
成本（元/台）	2200	2600
售价（元/台）	2800	3000

⑴冰箱厂有哪几种生产方案？
⑵该冰箱厂按哪种方案生产，才能使投入成本最少？“家电下乡”后农民买家电（冰箱、彩电、洗衣机）可享受售价13%的政府补贴，那么在这种方案下政府需补贴给农民多少元？
⑶若按⑵中的方案生产，冰箱厂计划将获得的全部利润购买三种物品：体育器材、实验设备、办公用品支援某希望小学．其中体育器材至多买4套，体育器材每套6000元，实验设备每套3000元，办公用品每套1800元，把钱全部用尽且三种物品都购买的情况下，请你直接写出实验设备的买法共有多少种．

已知：如图，点B在y轴的负半轴上，点A在x轴的正半轴上，且OA=2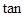，∠OAB=2。

（1）求点B的坐标；
（2）求直线AB的解析式；
（3）若点C的坐标为（-2,0），在直线AB上是否存在一点P，使ΔAPC与ΔAOB相似，若存在，求出点P的坐标；若不存在，请说明理由。

如图，在平面直角坐标系中，直线与轴交于点， 与轴交于点， 且，．点从点出发沿以每秒1个单位长的速度向点匀速运动，到达点后立刻以原来的速度沿返回；点从点出发沿以每秒1个单位长的速度向点匀速运动．伴随着、的运动，保持垂直平分，且交于点，交折线于点．点、同时出发，当点到达点时停止运动，点也随之停止．设点、运动的时间是秒（）．
（1）求直线的解析式；
（2）在点从向运动的过程中，求的面积与之间的函数关系式；
（3）在点从向运动的过程中，完成下面问题：
①四边形能否成为直角梯形？若能，请求出的值；若不能，请说明理由；
②当经过点时，请你直接写出的值．