[四川]2013届四川省仁寿县联谊学校九年级12月联考数学试卷
如图,已知坡面AB的坡度i=1∶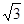 ,则坡角
,则坡角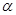 为( )
为( )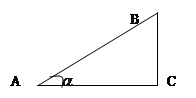
| A.15° | B.20° | C.30° | D.45° |
如图,每个大正方形均由边长为1的小正方形组成,则下列图中的三角形(阴影部分)与△ABC相似的是( )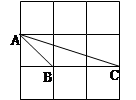

A. B. C. D.
关于x的方程 有实数根,则k的取值范围是( )
有实数根,则k的取值范围是( )
| A.k≤-1 | B.k≤1 | C.k≥-1且k≠0 | D.k≤1且k≠0 |
如图,P是Rt△ABC斜边AB上任意一点(A、B两点除外),过点P作一直线,使截得的三角形与Rt△ABC相似,这样的直线可以作( )
A、1条 B、2条 C、3条 D、4条
如图,在梯形ABCD中,AD∥BC,中位线EF与对角线BD交于点G。
若EG﹕GF=2﹕3,且AD=4,则BC的长是( )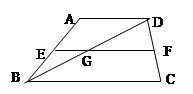
| A.3 | B.6 | C.8 | D.12 |
在“红桃5、红桃7、红桃9”这三张扑克牌中任取一张,抽到“红桃7”的概率是( )
| A.1 | B. |
C.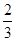 |
D.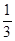 |
如图:EF是梯形ABCD的中位线,△DEF的面积为4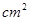 ,则梯形ABCD的面积为( )
,则梯形ABCD的面积为( )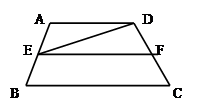
A.4 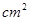 |
B.8 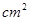 |
C.16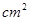 |
D.24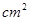 |
小明从家到学校要经过4个路口(都有红绿灯),我们知道“红灯停,绿灯行”,则小明从家到学校一路畅通无阻的概率是 .
为解决老百姓看病贵的问题,某药品经销商决定下调药品价格,某种药品经过两次调价,由每盒100元调至81元,则每次平均调价的百分率为
小明和小亮是一对双胞胎,他们的爸爸买了两套不同品牌的运动服送给他们,小明和小亮都想先挑选.于是小明设计了如下游戏来决定谁先挑选.游戏规则是:在一个不透明的袋子里装有除数字以外其它均相同的4个小球,上面分别标有数字1、2、3、4.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为奇数,则小明先挑选;否则小亮先挑选.
(1)用树状图或列表法求出小明先挑选的概率;
(2)你认为这个游戏公平吗?请说明理由.
如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1)。

(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍画出图形。
(2)写出B、C两点的对应点B´、C´的坐标;
(3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M´的坐标。
如图,小山的顶部是平地,在这块平地上有一高压输电线架,小山的斜坡BD的坡度i=1﹕ ,长度为50米。在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为60°。
,长度为50米。在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为60°。
求: ①小山的高度CE。
②铁架的高度AE。( ≈1.73,精确到0.1米)。
≈1.73,精确到0.1米)。
某商店如果将进货价为8元的商品按每件10元售出,每天可销售200件,现在采用提高售价,减少进货量的方法增加利润,已知这种商品每涨价1元,其销量就减少20件。
(1)要使每天获得利润700元,请你帮忙确定售价;
(2)问售价定在多少时能使每天获得的利润最多?并求出最大利润。
如图, ΔABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F。
(1)求证:ΔABD≌ΔBCE.
(2)ΔAEF与ΔABE相似吗?请说明理由.
(3) 成立吗?请说明理由.
成立吗?请说明理由.
 =5-x,那么x的取值范围是( )
=5-x,那么x的取值范围是( ) 是同类二次根式的是( )
是同类二次根式的是( )



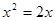 的根是( )
的根是( )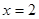
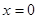
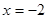
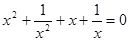 ,如果设
,如果设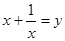 ,则原方程可变形为( )
,则原方程可变形为( )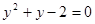
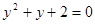
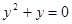
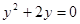
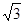
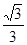
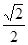
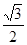
 ,则cosB =
,则cosB = 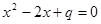 的一个根是1+
的一个根是1+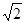 ,则另一根是____,
,则另一根是____,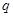 =_______
=_______ 、b在数轴上的位置如图所示,化简
、b在数轴上的位置如图所示,化简 =
= 



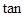 ∠OAB=2。
∠OAB=2。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号