浙江省杭州市萧山区南片八年级上12月质检数学试卷
下列四组线段中,能组成三角形的是( )
| A.2cm,3 cm,4 cm | B.3 cm,4 cm,8 cm |
| C.4 cm,6 cm,2 cm | D.7 cm,11 cm,2 cm |
在函数y=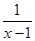 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
| A.x>1 | B.x<1 | C.x≠1 | D.x=1 |
在平面直角坐标系中,点(-1, )一定在( )
)一定在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
下列句子属于命题的是( )
| A.正数大于一切负数吗? | B.将16开平方 |
| C.钝角大于直角 | D.作线段AB的中点 |
如是用直尺和圆规作角平分线的示意图,通过证明△DOP≌△EOP可以说明OC是 ∠AOB的角平分线,那么△DOP≌△EOP的依据是( )

| A.SSS | B.SAS | C.ASA | D.AAS |
若正比例函数 的图象经过点
的图象经过点 和点
和点 ,当
,当 时,
时, ,则
,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
若方程组 的解x,y满足0<x+y<1,则k的取值范围是( )
的解x,y满足0<x+y<1,则k的取值范围是( )
| A.﹣1<k<0 | B.﹣4<k<0 | C.0<k<8 | D.k>﹣4 |
如图,点A的坐标为(-2,0),点B在直线y=x上运动,当线段AB最短时点B的坐为( )

| A.(-1,-1) | B.(-2,-2) | C.(- ,- ,- ) ) |
D.(0,0) |
如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列三个结论:①∠AOB=90°+  ②当∠C=90°时,E,F分别是AC,BC的中点;③若OD=a,CE+CF=2b,则S△CEF="ab" 其中正确的是( )
②当∠C=90°时,E,F分别是AC,BC的中点;③若OD=a,CE+CF=2b,则S△CEF="ab" 其中正确的是( )

| A.① | B.②③ | C.①② | D.①③ |
若一次函数y=-2x+1的图象经过平移后经过点(2,5),则需将此图象向 平移 单位.
已知函数y=ax+b和y=kx的图象交于点P,根据图象可得,求关于x的不等式ax+b>kx的解是____________.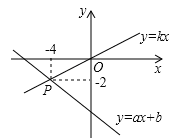
如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点B的坐标为(5,4),点P为线段BC上动点,当△POA为等腰三角形时,点p坐标为______________.

已知,如图,四边形ABCD,∠A=∠B=Rt∠
(1)用直尺和圆规,在线段AB上找一点E,使得EC=ED,连接EC,ED(不写作法,保留作图痕迹)
(2)在(1)的图形中,若∠ADE=∠BEC,且CE=3,BC= ,求AD的长.
,求AD的长.
已知平面直角坐标系中有一点M(m-1,2m+3)
(1)当m为何值时,点M到x轴的距离为1?
(2)当m为何值时,点M到y轴的距离为2?
如图,是一次函数y=kx+b的图象.
(1)求这个一次函数的解析式?
(2)试判断点P(1,-1)是否在这个一次函数的图象上?
(3)求原点O到直线AB的距离.
如图,已知在等腰直角三角形△DBC中,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF,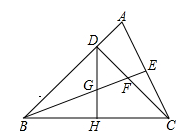
(1)试说明:△FBD≌△ACD;
(2)延长BF交AC于E,且BE⊥AC,试说明:CE=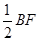
某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
该商场计划购进两种手机若干部,共需15.5万元,预计全部销售后可获毛利润共2.1万元.
(毛利润=(售价﹣进价)×销售量)
(1)该商场计划购进甲、乙两种手机各多少部?
(2) 通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.




 无解,则m的取值范围为_________.
无解,则m的取值范围为_________. 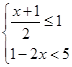 并把解集在数轴上表示出来。
并把解集在数轴上表示出来。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号