如图,已知反比例函数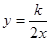 和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+1,b+k)两点.
和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+1,b+k)两点.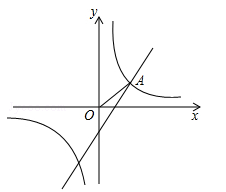
(1)求反比例函数的解析式;
(2)如图,已知点A在第一象限,且同时在上述两个函数的图象上,求点A的坐标;
(3)利用(2)的结果,请问:在x轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由.
推荐套卷
如图,已知反比例函数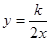 和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+1,b+k)两点.
和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+1,b+k)两点.
(1)求反比例函数的解析式;
(2)如图,已知点A在第一象限,且同时在上述两个函数的图象上,求点A的坐标;
(3)利用(2)的结果,请问:在x轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由.