钓鱼岛是我国渤海海峡上的一颗明珠，渔产丰富．一天某渔船离开港口前往该海域捕鱼．捕捞一段时间后，发现一外国舰艇进入我国水域向钓鱼岛驶来，渔船向渔政部门报告，并立即返航．渔政船接到报告后，立即从该港口出发赶往钓鱼岛．下图是渔船及渔政船与港口的距离s和渔船离开港口的时间t之间的函数图象．（假设渔船与渔政船沿同一航线航行）
（1）直接写出渔船离港口的距离s和它离开港口的时间t的函数关系式．
（2）求渔船和渔政船相遇时，两船与钓鱼岛的距离．
（3）在渔政船驶往钓鱼岛的过程中，求渔船从港口出发经过多长时间与渔政船相距30海里？
如图，A（0，1），M（3，2），N（4，4），动点P从点A出发，沿y轴以每秒1个单位长的速度向上移动，且过点P的直线l：y＝－x+b也随之移动，设移动时间为t秒．（直线y = kx+b平移时k不变）
（1）当t＝3时，求l的解析式；
（2）若点M，N位于l的异侧，确定 t 的取值范围．
已知一次函数y=kx+b的图象经过点（-1，-5），且与正比例函数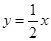
的图象相交于点（2，a）．
（1）求a的值．
（2）求一次函数y=kx+b的表达式．
（3）在同一坐标系中，画出这两个函数的图象．
某商店积压了100件某种商品，为使这批货物尽快脱手，该商店采取了如下销售方案，将价格提高到原来的2．5倍，再作3次降价处理；第一次降价30％，标出“亏本价”；第二次降价30％，标出“破产价”；第三次降价30%，标出“跳楼价”．3次降价处理销售结果如下表：
| 降价次数 |
一 |
二 |
三 |
| 销售件数 |
10 |
40 |
一抢而光 |
（1）跳楼价占原价的百分比是多少?
（2）该商品按新销售方案销售，相比原价全部售完，哪种方案更盈利?
本市出租车的收费标准为：3千米以内（含3千米）收费5元，超过3千米的部分每千米收费1．20元（不足1千米按1千米计算），另加收0．60元的返空费．
（1）设行驶路程为x千米（
≥3且取整数），用x表示出应收费y元的代数式；
（2）当收费为10．40元时，该车行驶路程不超过多少千米？路程数在哪个范围内？
如图，直线PA经过点A（-1，0）、点P（1，2），直线PB是一次函数y=-x+3的图象．
（1）求直线PA的表达式及Q点的坐标；
（2）求四边形PQOB的面积；
重庆某餐饮集团公司将沙坪坝下属一个分公司对外招商承包，有符合条件的两个企业甲、乙，分别拟定上缴利润方案如下：
甲：每年结算一次上缴利润，第一年上缴利润5万元，以后每年比前一年增加5万元；
乙：每半年结算一次上缴利润，第一个半年上缴利润1．5万元，以后每半年比前一半年增加1．5万元；
（1）如果企业乙承包一年，则需上缴的总利润为万元．
（2）如果承包4年，你认为应该承包给哪家企业，总公司获利多？为什么？
（3）如果承包n年，请你用含n的代数式分别表示两企业上缴利润的总金额（单位：万元）．
盘锦红海滩景区门票价格80元/人，景区为吸引游客，对门票价格进行动态管理，非节假日打a折，节假日期间，10人以下（包括10人）不打折，10人以上超过10人的部分打b折，设游客为x人，门票费用为y元，非节假日门票费用
（元）及节假日门票费用
（元）与游客x（人）之间的函数关系如图所示．
（1）a= ，b= ；
（2）直接写出、与x之间的函数关系式；
（3）导游小王6月10日（非节假日）带A旅游团，6月20日（端午节）带B旅游团到红海滩景区旅游，两团共计50人，两次共付门票费用3040元，求A、B两个旅游团各多少人？
某电信公司手机的A类收费标准如下：每部手机每月缴纳月租50元，另外每通话1分钟缴费0．4元；B类收费标准如下：没有月租费，但每通话1分钟缴费0．6元．
（1）分别写出手机A、B两类收费标准每月应缴纳费用y（元）与通话时间x之间的关系．
（2）一个用户这个月预缴花费200元，按A ，B两类手机收费标准分别可以通话多长时间．
（3）若用户每月平均通话时间300分钟，会选择哪种收费方式？
如图，一次函数y=kx+2的图像经过点A（2，4），与x轴交于点C，求直线AC的函数解析式及△AOC的面积．
如图，已知函数y=x+1的图象与y轴交于点A，一次函数y=kx+b的图象经过点B（0，-1），与x轴以及y=x+1的图象分别交于点C、D，且点D的坐标为（1，n），
（1）点A的坐标是 ，n= ，k= ，b= ；
（2）x取何值时，函数y=kx+b的函数值大于函数y=x+1的函数值；
（3）求四边形AOCD的面积；
（4）是否存在y轴上的点P，使得以点P，B，D为顶点的三角形是等腰三角形？若存在求出点P的坐标；若不存在，请说明理由．
某气象研究中心观测一场沙尘暴从发生到结束全过程，开始时风暴平均每小时增加2千米/时，4小时后，沙尘暴经过开阔荒漠地，风速变为平均每小时增加4千米/时，一段时间，风暴保持不变，当沙尘暴遇到绿色植被区时，其风速平均每小时减小1千米/时，最终停止．结合风速与时间的图象，回答下列问题：
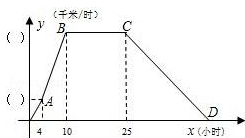
（1）在y轴（ ）内填入相应的数值；
（2）沙尘暴从发生到结束，共经过多少小时？
（3）求出当x≥25时，风速y（千米/时）与时间x（小时）之间的函数关系式；
（4）若风速达到或超过20千米/时，称为强沙尘暴，则强沙尘暴持续多长时间？
已知直线y=kx+b经过点A（5，0），B（1，4）．
（1）求直线AB的解析式；
（2）若直线y=2x-4与直线AB相交于点C，求点C的坐标；
（3）根据图象，写出关于x的不等式2x-4＞kx+b的解集．
已知一次函数y=kx+b的图象经过点（-2，-4），且与正比例函数
的图象相交于点（4，a），求：
（1）a的值；
（2）k、b的值；
（3）画出这两个函数图象，并求出它们与y轴相交得到的三角形的面积．
粤公网安备 44130202000953号
