甲、乙两组工人同时加工某种零件,乙组工作中有一次停产更换设备,更换
设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量 (件)与时间
(件)与时间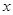 (时)的函数图象如图所示.
(时)的函数图象如图所示.
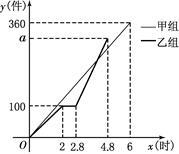
(1)求甲组加工零件的数量y与时间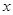 之间的函数关系式.
之间的函数关系式.
(2)当x=2.8时,甲、乙两组共加工零件 件;乙组加工零件总量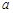 的值为 .
的值为 .
(3)加工的零件数达到230件装一箱,零件装箱的时间忽略不计,若甲、乙两组加工出的零件合在一起装箱,当甲组工作多长时间恰好装满第2箱?
相关知识点
推荐套卷
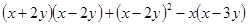 ]÷
]÷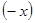
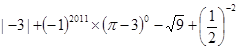
 ABC的角平分线,PM
ABC的角平分线,PM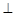 AB于M,PN
AB于M,PN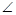 AOD与
AOD与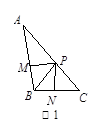
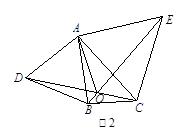
 和x>20时y与x的函数表达式;
和x>20时y与x的函数表达式;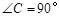 ,请用直尺和圆规作一条直线,把△ABC分割成两个等腰三角形,并在图上标出分割成的等腰三角形的底角的度数.(不写作法,但须保留作图痕迹);
,请用直尺和圆规作一条直线,把△ABC分割成两个等腰三角形,并在图上标出分割成的等腰三角形的底角的度数.(不写作法,但须保留作图痕迹);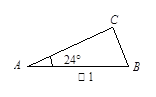
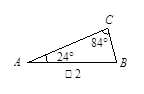
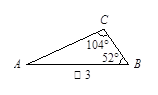
 粤公网安备 44130202000953号
粤公网安备 44130202000953号