在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.观察图中每一个正方形(实线)四条边上的整点的数.
(1)画出由里向外的第 个正方形,求在第四个正方形边上有多少个整点?
(2)请你猜测由里向外第 个正方形(实线)四条边上的整点共有多少个;
(3)探究点 在由里向外的第几个正方形的边上,点 在由里向外的第几个正方形的边上.
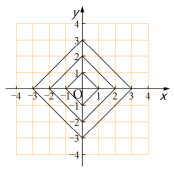
在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.观察图中每一个正方形(实线)四条边上的整点的数.
(1)画出由里向外的第 个正方形,求在第四个正方形边上有多少个整点?
(2)请你猜测由里向外第 个正方形(实线)四条边上的整点共有多少个;
(3)探究点 在由里向外的第几个正方形的边上,点 在由里向外的第几个正方形的边上.
