初中数学一次函数的最值解答题

如图，一个正比例函数的图象和一个一次函数的图象交于点A（－1，2），且△ABO 的面积为 5，求这两个函数的解析式。

如图，已知直线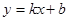与x轴点A（-4，0），与y轴交于点B，与双曲线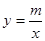交于点C（a，3）和点D，且.

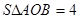（1）求直线AB和双曲线的表达式；
（2）若CE⊥x轴于点E，连接DE.求⊿CDE的面积.

如图，在平面直角坐标系中，点A在第一象限，点B的坐标为（3，0），OA=2，。
（1）求点A的坐标；
（2）若直线AB交y轴于点C，求的面积。

已知一次函数的图象经过点A（-2，-3）及点B（1，6）.
（1）求此一次函数的解析式.
（2）判断点C(,2)是否在函数的图象上.

已知汽车油箱中有油40升，汽车每行驶1小时消耗5升油，求油箱中的余油量Q（升）与行驶时间t（小时）之间的函数关系，并作出函数的图象。

已知一次函数图像经过点A（1，-1）和B（-3，-9）。（1）求此一次函数的解析式；
（2）求此一次函数与x轴,y轴的交点坐标。

已知，一次函数和的图像交于点A（-1，m）
⑴求出m,b的值；
⑵求出这两条直线与x轴围成的图形的面积。

已知A（6， 0）及在第一象限的动点P（x， y），且x+y=8，设△OPA的面积为S 

（1）求S关于x的函数解析式及x的取值范围
（2）求S=10时，P的坐标
（3）画出函数S的图像

已知与成正比例函数关系，且时，。
（1）写出与之间的函数关系式；
（2）求当时，的值；
（3）求当时，的值。

已知一次函数．
（1）画出该函数的图象；
（2）根据图象回答：当x取何值时，y＞0？

如图，在平面直角坐标系中，函数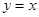的图象是第一、三象限的角平分线．
实验与探究：由图观察易知A（0，2）关于直线的对称点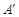的坐标为（2，0），请在图中分别标明B(5,3) 、C(-2,5) 关于直线的对称点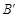、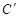的位置，并写出它们的坐标:              、          ；
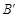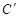归纳与发现：结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P(m,n)关于第一、三象限的角平分线的对称点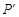的坐标为           ；
运用与拓广：已知两点D(0,-3)、E(-1,-4)，试在直线上确定一点Q，使点Q到D、E两点的距离之和最小，并求出Q点坐标．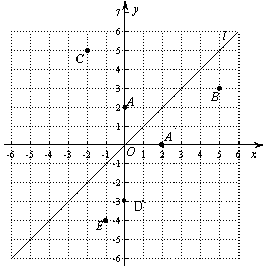

如图，在平面直角坐标系中,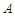、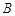均在边长为1的正方形网格格点上．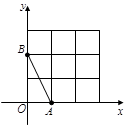

(1)若点P在图中所给网格中的格点上，△APB是等腰三角形，满足条件的点P共有            个．
(2)将线段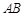沿x轴向右平移2格得线段CD，请你求出线段CD所在的直线函数解析式．

若一次函数y=-2x+b的图像经过点（2，2）.（1）求b的值；（2）在图中画出此函数的图像；（3）观察图像，直接写出y<0时x的取值范围.

已知一次函数图象经过点(3 , 5) , (–4，–9)两点.
(1)求一次函数解析式.
(2)求图象和坐标轴围成三角形面积.

已知函数y=(2m–2)x+m+1
(1)m为何值时，图象过原点.         
(2)已知y随x增大而增大，函数图象与y轴交点在x轴上方，求m取值范围.