初中数学一次函数的最值解答题

某电信公司给顾客提供了两种手机上网计费方式：方式A以每分钟0.1元的价格按上网时间计费；方式B除收月基费20元外，再以每分钟0.06元的价格按上网时间计费．假设顾客甲一个月手机上网的时间共有分钟，上网费用为元．
（1）分别写出顾客甲按A、B两种方式计费的上网费元与上网时间分钟之间的函数关系式，并在下图的坐标系中作出这两个函数的图象；

（2）如何选择计费方式能使上网费更合算？

问题情境：
用同样大小的黑色棋子按如图所示的规律摆放，则第2012个图共有多少枚棋子？

建立模型：
有些规律问题可以借助函数思想来探讨，具体步骤：第一步，确定变量；第二步：在直角坐标系中画出函数图象；第三步：根据函数图象猜想并求出函数关系式；第四步：把另外的某一点代入验证，若成立，则用这个关系式去求解．
解决问题：
根据以上步骤，请你解答“问题情境”．

A市和B市库存某种机器分别为12台和6台，现决定支援给C市10台和D市8台，已知从A市调运一台机器到C市和D市的运费分别为400元和800元，从B市调运一台机器到C市和D市的运费分别为300元和500元。
设B市运往C市的机器x台，求总运费W（元）与x的函数式。
若要求总运费不超过9000元，问：共有几种调运方案。
请选择最佳调运方案，使总运费最少，并求出最少总运费。

已知直线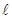经过点A(1，－1)，且与直线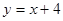交于点B(m，3)。
求点B的坐标。
求直线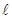的函数解析式。

如图，已知一次函数y=kx+b的图象交反比例函数的图像交于点A、B，交x轴于点C．
求m的取值范围；
若点A的坐标是（2，-4），且，求m的值和一次函数的解析式；
根据图像，写出当反比例函数的值小于一次函数的值时x 的取值范围？

已知一次函数
（1）若这个函数的图象经过原点，求m的值；
（2）若这个函数是一次函数，且y随着x的增大而减小，求m的取值范围；
（3）若这个函数的图象不经过第二象限，求m的取值范围.

若与－1成正比例，＝4时，＝6.写出y与x之间的函数关系式，并画出该函数的图象.

已知直线与x轴交于点A，与y轴交于点B，O为坐标原点，求△AOB的面积.

某风景区团体门票的收费标准：20人以内（含20人），每人25元；超20人，超过部分，每人10元.
（1）写出应收门票y（元）与游览人数x（人）（>20）之间的函数关系式；
（2）若某班有54名同学去该风景区游览，为购门票共花了多少钱？

如图，点P（－3，1）是反比例函数的图象上的一点.

求该反比例函数的解析式；
设直线与双曲线的两个交点分别为P和P′，
当＜时，直接写出x的取值范围．

平安加气站某日的储气量为10000立方米．假设加气过程中每把加气枪均以每小时200立方米的速度为汽车加气．设加气站的储气量为y（立方米），加气总时间为x（小时）（加气期间关闭加气枪的时间忽略不计）．从7︰00开始，加气站加气枪的使用数量如下表所示：

时间段	7︰00—7︰30]	7︰30—8︰00	8︰00以后
加气枪使用︰数量 （单位：把）	3	5	6

分别求出7︰00—7︰30及8︰00之后加气站的储气量y（立方米）与时间x（小时）的函数关系式．
若每辆车的加气量均为20立方米，请通过计算说明前50辆车能否在当天8︰00之前加完气．

随着生活水平的逐步提高，某单位的私家小轿车越来越多，为确保有序停车，单位决定筹集资金维修和新建一批停车棚．该单位共有42辆小轿车，准备维修和新建的停车棚共有6个，费用和可供停车的辆数及用地情况如下表：

停车棚	费用（万元/个）	可停车的辆数（辆/个）	占地面积（m^2/个）
新建	4	8	100
维修	3	6	80

已知可支配使用土地面积为580m²，若新建停车棚个，新建和维修的总费用为万元．
求与之间的函数关系
满足要求的方案有几种？
为确保工程顺利完成，单位最少需要出资多少万元

已知，点P(x，y)在第一象限，且x+y=12，点A(10，0)在x轴上，设△OPA的面积 为S．
求S关于x的关系式，并确定x的取值范围；
当△OPA为直角三角形时，求P点的坐标．
                    

如图1，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A的坐标为（－3，4），点C在x轴的正半轴上，直线AC交y轴于点M，AB边交y轴于点H．

（1）求直线AC的解析式；
（2）连接BM，如图2，动点P从点A出发，沿折线ABC方向以2个单位／秒的速度向终点C匀速运动，设△PMB的面积为S（S≠0），点P的运动时间为t秒，求S与t之间的函数关系式（要求写出自变量t的取值范围）；
（3）在（2）的条件下，当 t为何值时，∠MPB与∠BCO互为余角．

市园林处为了对一段公路进行绿化，计划购买A、B两种风景树共900棵。若购买A树x棵，所需总费用y元. B两种树的相关信息如下表：
A、
求y与x之间的函数关系式.
若购树的总费用不超过82000元，则购A种树不少于多少棵？
若希望这批树的成活率不低于94%，且使购树的总费用最低，应选购A、B两
种树各多少棵？此时最低费用为多少？