初中数学一次函数的最值解答题

如图，已知一次函数的图像与轴，轴分别交于A（1，0）、B（0，－1）两点，且又与反比例函数的图像在第一象限交于C点，C点的横坐标为2.

求一次函数的解析式；
求C点坐标及反比例函数的解析式

如图，在平面直角坐标系中，A、B均在边长为1的正方形网格格点上．

求线段AB所在直线的函数关系式，并写出当0≤y≤2时，自变量x的取值范围；
将线段AB绕点B逆时针旋转90°，得到线段BC，若直线BC的函数关系式为y=kx+b，则y随x的增大而      （填“增大”或“减小”）．

如图在平面直角坐标系中，A点坐标为（8，0），B点坐标为（0，6）C是线段AB的中点。请问在y轴上是否存在一点P，使得以P、B、C为顶点的三角形与△AOB相似？若存在，求出P点坐标；若不存在，说明理由。

如图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图像．根据图像解答下列问题：
在轮船快艇中，哪一个的速度较大？
通过计算回答：当时间x在什么范围内时，快艇在轮船的后面？当时间x在什么范围内时，快艇在轮船的前面？

如图，一次函数y＝k₁x＋b的图象经过

A（0，－2），B（1，0）两点，与反比例函数的
图象在第一象限内的交点为M，若△OBM的面积为2．
（1）求一次函数和反比例函数的表达式；
（2）在x轴上是否存在点P，使AM⊥MP？若存在，
求出点P的坐标；若不存在，说明理由．

如图，一次函数的图象与反比例函数的图象交于A、B两点．

(1)利用图中条件，求反比例函数和一次函数的解析式；
(2)根据图象求出使一次函数的值大于反比例函数的值时，x的取值范围．

今年，号称“千湖之省”的湖北正遭受大旱，为提高学生环境意识，节约用水，某校数学教师编制了一道应用题：
为了保护水资源，某市制定一套节水的管理措施，其中对居民生活用水收费作如下规定：

月用水量（吨）	单价（元/吨）
不大于10吨部分	1.5
大于10吨不大于吨部分()	2
大于吨部分	3

（1）若某用户六月份用水量为18吨，求其应缴纳的水费；
（2）记该用户六月份用水量为吨，缴纳水费为元，试列出与的函数式；
（3）若该用户六月份用水量为40吨，缴纳水费元的取值范围为，试求的取值范围。

某地举办乒乓球比赛的费用（元）包括两部分：一部分是租用比赛场地等固定不变的费用（元），另一部分费用与参加比赛的人数（人）成正比。当=20时，=1600；当=30时，=2000；
1）求与之间的函数关系式
2）如果承办此次比赛的组委会共筹集到经费6250元，那么这次比赛最多可邀请多少名运动员参赛？

已知一纸箱中放有大小均匀的只白球和只黄球，从箱中随机地取出一只白球的概率是．
写出与的函数关系式；
当时，再往箱中放进20只白球，求随机地取出一只黄球的概率．

已知某种水果的批发单价与批发量的函数关系如图（1）所示．
请说明图中①、②两段函数图象的实际意义；
写出批发该种水果的资金金额w（元）与批发量n（kg）之间的函数关系式；在下图的坐标系中画出该函数图象；指出金额在什么范围内，以同样的资金可以批发到较多数量的该种水果.
经调查，某经销商销售该种水果的日最高销量与零售价之间的函数关系如图（2）所示，该经销商拟每日售出60kg以上该种水果，且当日零售价不变，请你帮助该经销商设计进货和销售的方案，使得当日获得的利润最大．

A、B两城间的公路长为450千米，甲、乙两车同时从A城出发沿这一公路驶向B城，甲车到达B城1小时后沿原路返回．如图是它们离A城的路程y（千米）与行驶时间 x（小时）之间的函数图像．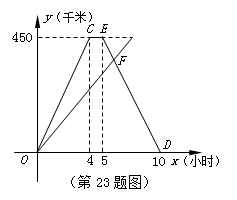

（1）求甲车返回过程中y与x之间的函数解析式，并写出x的取值范围；
（2）乙车行驶6小时与返回的甲车相遇，求乙车的行驶速度．

（本小题10分）某通讯器材公司销售一种市场需求较大的新型通讯产品,已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120万元.在销售过程中发现单价为60元时,年销售量可达5万件;若价格上涨,相应销量就会减少;当单价为80元时,销售量降至4万件,设销售单价为元.( >60)
①.用含x的代数式表示出年销售量; 
②.当单价定为多少元时,年销售获利可达40万元?
③.当销售单价x为何值时,年获利最大?并求出这个最大值.

为了增强居民的节约用水意识，某市制定了新的水费收费标准：每户每月不超过5吨的部分，自来水公司按每吨2元收费；超过5吨部分，按每吨2.6元收费．设某用户月用水量为x吨，自来水公司应收水费y元．
(1)试写出y(元)与x(吨)之间的函数关系式；
(2)该用户今年5月份的用水量为8吨，自来水公司应收水费多少元？

．直线：与经过点（3，-5）的直线关于轴对称，求直线的解析式。

作出函数的图象，并根据图象回答下列问题：

（1）y的值随x的增大而      ；
（2）图象与x轴的交点坐标是        ；与y轴的交点坐标是      ；
（3）当x      时，y≥0 ；
（4）函数的图象与坐标轴所围成的三角形的面积是多少？