初中数学一次函数的最值解答题

已知一次函数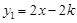的图象与反比例函数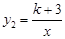的图象相交，其中一个交点的纵坐标为-4．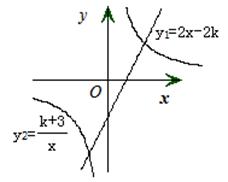

求两个函数的解析式
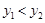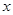结合图象求出当时，的取值范围

已知一次函数，问：（1）m为何值时，函数图像平行于直线y=2x?     (2)、m为何值时，函数图像与y轴交与（0，—3）点？

如图，直线L₁的表达式为y=-3x+3,且与x轴交于点D.直线L₂经过点
A（4,0），B（3，-），直线L₁、L₂交于点C.
（1）求点D的坐标；
（2）求直线L₂的函数表达式；
（3）求△ADC的面积.

已知y-1与x成正比例，且当x=-1时，y=3.
（1）求y与x的函数解析式；
（2）当y=-7时，求x的值.

对于气温，有的地方用摄氏温度表示，有的地方用华氏温度表示，摄氏温度与华氏温度之间存在一次函数关系．从温度计的刻度上可以看出，摄氏温度x（℃）与华氏温度y（℉）有如下的对应关系：

x（℃）	…	－10	0	10	20	30	…
y（℉）	…	14	32	50	68	86	…

（1）试确定y与x之间的函数关系式；
（2）若银川某天的华氏温度为77℉，那么银川这天的摄氏温度是多少？

如图，直线：、直线：相交于点A（4，4）,直线经过点（0，2）.

（1）求直线的函数关系式；
（2）求的值；
（3）

如图，一次函数的图象与反比例函数的图象相交于A、B两点．
求出这两个函数的解析式；
结合函数的图象回答：当自变量x的取值范围满足什么条件时，？

如图，直线：与直线：相交于点．
求的值；
不解关于的方程组                请你直接写出它的解；
直线：是否也经过点？请说明理由．

小华观察钟面（图1），了解到钟面上的分针每小时旋转360度，时针毎小时旋转30度．他为了进一步探究钟面上分针与时针的旋转规律，从下午2：00开始对钟面进行了一个小时的观察．为了探究方便，他将分针与分针起始位置OP（图2）的夹角记为y₁，时针与OP的夹角记为y₂度（夹角是指不大于平角的角），旋转时间记为t分钟．观察结束后，他利用获得的数据绘制成图象（图3），并求出y₁与t的函数关系式：
请你完成：
求出图3中y₂与t的函数关系式；
直接写出A、B两点的坐标，并解释这两点的实际意义；
若小华继续观察一个小时，请你在题图3中补全图象．

已知与成正比例，且当时，；
（1）写出与之间的函数关系式；
（2）当时，求的值；

( 本题8分) 已知函数的图象经过点(- 3, - 2)及点(1, 6).
(1) 求此一次函数解析式,并画图象;
(2) 求此函数图象与坐标轴围成的三角形的面积.

（本题8分）阅读下面的材料：
在平面几何中，我们学过两条直线平行的定义．下面就两个一次函数的图象所确定的两条直线，给出它们平行的定义：设一次函数y=k₁x+b₁（k₁≠0）的图象为直线L₁，一次函数y=k₂x+b₂（k₂≠0）的图象为直线L₂，若k₁=k₂，且b₁≠b₂，我们就称直线L₁与直线L₂互相平行．解答下面的问题：
（1）求过点P（1，4），且与直线y=－2x－1平行的直线L的函数解析式，并画出直线L的图象；
（2）设直线L分别与y轴，x轴交于点A，B，如果直线m：y=kx+t（t＞0）与直线L平行，且交x轴于点C，求出△ABC的面积S关于t函数解析式．
 

．
若方程组的解所对应的点在一次函数的图象上，求的值.

、(8分)已知一次函数y=Kx+b的图象过点(3，5)与(－4，－9)，
（1）求这个一次函数解析式。
（2）利用函数图象求当x为何值时，y>0。

学习一次函数时，老师直接告诉大家结论：“直线y=kx＋b在平移时，k不变”.爱思考的小张同学在平面直角坐标系中任画了一条直线y=kx＋b交x、y轴于B、A两点，假设直线向右平移了a个单位得到y=k₁x＋b₁，请你和他一起探究说明一下k₁=k.