初中数学一次函数的最值解答题

已知一次函数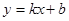的图像经过点（－2，4）且与直线平行，求这个一次函数的解析式。

已知一次函数的图像过点(-2，5)且它与y轴的交点和直线y=与y轴的交点关于x轴对称，求这个一次函数的解析式。

已知y是x的一次函数，且当x=2时，y= -1，x=0时，y= -5.
试求出y与x的函数关系式。

某人从离家18千米的地方返回，他离家的距离s(千米)与时间t(分钟)的函数图象如图所示：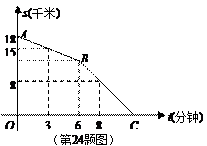

求线段AB的解析式
求此人回家用了多长时间？

已知正方形ABCD的边长是2，E是CD的中点，动点P从点A出发，沿A→B→C→E运动，到达E点即停止运动，若点P经过的路程为x，△APE的面积记为y，试求出y与x之间的函数解析式，并求出当y＝时，x的值．

某市政府大力扶持大学生创业．李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：．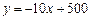
设李明每月获得利润为W（元），当销售单价定为多少元时，每月可获得最大利润？
如果李明想要每月获得2000元的利润，那么销售单价应定为多少元？
根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果李明想要每月获得的利润不低于2000元，那么他每月的成本最少需要多少元？（成本＝进价×销售量）

(8分)一根祝寿蜡烛长85cm,点燃时每小时缩短5cm。
（1）请写出点燃后蜡烛的长y(cm)与蜡烛燃烧时间t（h）之间的函关系式；
（2）该蜡烛可点燃多长时间？

水箱的最大盛水量为100升，水箱内原有水20升，现以每分钟2升的速度向水箱灌水。
（1）求水箱中存水量y和灌水时间x之间的函数解析式和自变量x的取值范围，并画出图像；
（2）当灌水时间为10分钟时，水箱内有多少升水？

已知弹簧的长度y（厘米）在一定的限度内是所挂物质量x（千克）的一次函数．现已测得不挂重物时弹簧的长度是6厘米，挂4千克质量的重物时，弹簧的长度是7. 2厘米,求这个一次函数的关系式．

已知与成正比例,且时,.
(1)求与的函数关系式;
(2)当时,求的值;
(3)将所得函数图象平移,使它过点(2,-1).求平移后直线的解析式.

已知直线经过点（1，2）和点（，4），求这条直线的解析式.

某地拔号入网有两种收费方式，A计时制3元/时，B全日制54元/月，另加通信费1.2元/时，问选择哪种上网方式省钱？

已知一次函数图象经过（3，5）和（-4，-9）两点，（1）求此一次函数解析式；（2）若点在（a，2）函数图象上，求a的值。

等腰三角形周长40cm.（1）、写出底边长ycm与腰xcm的函数关系式.
（2）、写出自变量取值范围.（3）、画出函数图象

直线y=2x+m和直线y=3x+3的交点在第二象限，求m的取值范围.