如图，在平面直角坐标系中，A、B均在边长为1的正方形网格格点上．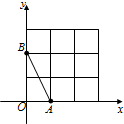
求线段AB所在直线的函数关系式，并写出当0≤y≤2时，自变量x的取值范围；
将线段AB绕点B逆时针旋转90°，得到线段BC，若直线BC的函数关系式为y=kx+b，则y随x的增大而 （填“增大”或“减小”）．
相关试题
的图象与反比例函数
的图象交于点A（3，2）.
过点M作直线MB∥x轴，交y轴于点B；过点A作直线AC∥y轴，交x轴于点C，交直线MB于点D.当四边形OADM的面积为6时，请判断线段MB与DM的大小关系，并说明理由.相关知识点
推荐套卷
如图，在平面直角坐标系中，A、B均在边长为1的正方形网格格点上．求线段AB所在直线的函数关系式，并写出当0≤y≤2时，自变量x的取值范围；
将线段AB绕点B逆时针旋转90°，得到线段BC，若直线BC的函数关系式为y=kx+b，则y随x的增大而 （填“增大”或“减小”）．
粤公网安备 44130202000953号