已知二次函数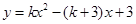 在
在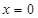 和
和 时的函数值相等.
时的函数值相等.
(1)求该二次函数的表达式;
(2)画出该函数的图象,并结合图象直接写出当 时,自变量
时,自变量 的取值范围;
的取值范围;
(3)已知关于 的一元二次方程
的一元二次方程 ,当
,当 时,判断此方程根的情况.
时,判断此方程根的情况.
相关知识点
推荐套卷
已知二次函数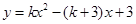 在
在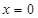 和
和 时的函数值相等.
时的函数值相等.
(1)求该二次函数的表达式;
(2)画出该函数的图象,并结合图象直接写出当 时,自变量
时,自变量 的取值范围;
的取值范围;
(3)已知关于 的一元二次方程
的一元二次方程 ,当
,当 时,判断此方程根的情况.
时,判断此方程根的情况.