[江苏]2012届江苏省南京市六合区中考一模数学试卷
一种病毒长度约为0.000058 mm,用科学记数法表示这个数为( )
A.5.8×10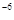 |
B. 5.8×10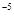 |
C.0.58×10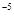 |
D.58×10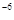 |
在下列图形中,既是轴对称图形,又是中心对称图形的是( )



直角三角形 正五边形 正方形 等腰梯形
| A. | B. | C. | D. |
如图,A是反比例函数 图象上一点,过点A作AB⊥x轴于点B,点P在y轴上,△ABP的面积为1,则k的值为( )
图象上一点,过点A作AB⊥x轴于点B,点P在y轴上,△ABP的面积为1,则k的值为( )
| A.1 | B.2 | C.-1 | D.-2 |

在一个不透明的口袋中装有若干个只有颜色不同的球,如果口袋中装有4个红球,且摸出红球的概率为 ,那么袋中其它颜色的球有 个
,那么袋中其它颜色的球有 个
如图,点A1、B1、C1分别是△ABC的三边BC、AC、AB的中点,点A2、B2、C2分别是△A1B1C1的边B1C1、A1C1、A1B1的中点,依此 类推,则△AnBnCn与△ABC的面积比为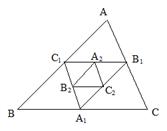
为了了解某校九年级学生的体质健康状况,从该校九年级学生中随机抽取了40名学生进行调查.将调查结果绘制成如下统计表和统计图.请根据所给信息解答下列问题:]
| 成绩 |
频数 |
频率 |
| 不及格 |
3 |
0.075 |
| 及格 |
|
0.2 |
| 良好 |
17 |
0.425 |
| 优秀 |
|
|
| 合计 |
40 |
1 |

补充完成频数统计表;
求出扇形统计图的“优秀”部分的圆心角度数;
若该校九年级共有200名学生,试估计该校体质健康状况达到良好及以上的学生总人数.
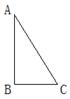
如图,在△ABC中,AB=AC.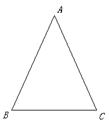
作∠BAC的角平分线,交BC于点D(尺规作图,保留痕迹);
在AD的延长线上任取一点E,连接BE、CE. 求证:△BDE≌△CDE;
当AE=2AD时,四边形ABEC是菱形.请说明理由.
已知正比例函数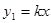 (k≠0)和反比例函数
(k≠0)和反比例函数 的图象都经过点(-2,1).
的图象都经过点(-2,1).求这两个函数的表达式;
试说明当x为何值时,

有3张背面相同的卡片,正面分别写着数字“1”、“2”、“3”.将卡片洗匀后背面朝上放在桌面上.若小明从中任意抽取一张,则抽到奇数的概率是 ;
若小明从中任意抽取一张后,小亮再从剩余的两张卡片中抽取一张,规定:抽到的两张卡片上的数字之和为奇数,则小明胜,否则小亮胜.你认为这个游戏公平吗?请用 画树状图或列表的方法说明你的理由.
已知二次函数 (m为常数).
(m为常数).求证:不论m为何值,该二次函数图象的顶点P都在函数
 的图象上;
的图象上;若顶点P的横、纵坐标相等,求P点坐标
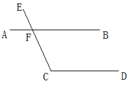
多年来,许多船只、飞机都在大西洋的一个区域内神秘失踪,这个区域被称为百
慕大三角.根据图中标出的百慕大三角的位置及相关数据计算:∠BAC的度数;
百慕大三角的面积.
(参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)
点D是⊙O的直径CA延长线上一点,点B在⊙O上,∠DBA=∠C.请判断BD所在的直线与⊙O的位置关系,并说明理由;
若AD=AO=1,求图中阴影部分的面积(结果保留根号).

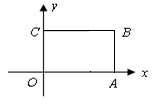
如图,在平面直角坐标系中,点A,B的坐标分别为A(2,4),B(4,0).以原点O为位似中心,把线段AB缩小为原来的
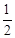 ;
;若(1)中画出的线段为
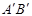 ,请写出线段
,请写出线段 两个端点
两个端点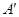 ,
, 的坐标;
的坐标;若线段AB上任意一点M的坐标为(a,b),请写出缩小后的线段
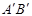 上对应点
上对应点 的坐标.
的坐标.
观察猜想
如图,大长方形是由四个小长方形拼成的,请根据此图填空: =
=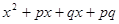 = ( )( ).
= ( )( ).
说理验证
事实上,我们也可以用如下方法进行变形: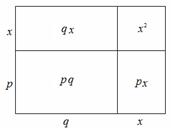
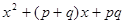 =
=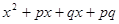 =
=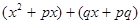
= =( )( ).
于是,我们可以利用上面的方法进行多项式的因式分解.
尝试运用
例题 把 分解因式.
分解因式.
解: =
= =
= .
.
请利用上述方法将下列多项式分解因式: ;
;  .
.
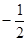

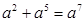


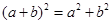
 =
=
 中,自变量
中,自变量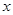 的取值范围是
的取值范围是
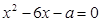 没有实数根,则a的取值范围是
没有实数根,则a的取值范围是 ,并判断x=
,并判断x= 是否为此不等式组的解.
是否为此不等式组的解. ,再选择一个恰当的数作为x的值代入求值.
,再选择一个恰当的数作为x的值代入求值.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号