阅读以下材料,并解答以下问题.
“完成一件事有两类不同的方案,在第一类方案中有m种不同的方法,在第二类方案中有n种不同的方法.那么完成这件事共有N=" m" + n种不同的方法,这是分类加法计数原理;完成一件事需要两个步骤,做第一步有m种不同的方法,做第二步有n种不同的方法.那么完成这件事共有N=m×n种不同的方法, 这就是分步乘法计数原理. ”如完成沿图1所示的街道从A点出发向B点行进这件事(规定必须向北走,或向东走), 会有多种不同的走法,其中从A点出发到某些交叉点的走法数已在图2填出.
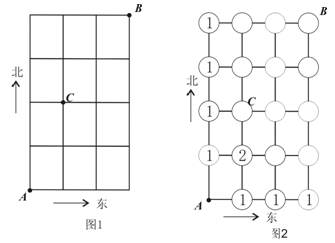
(1)根据以上原理和图2的提示, 算出从A出发到达其余交叉点的走法数,将数字填入图2的空圆中,并回答从A点出发到B点的走法共有多少种?
(2)运用适当的原理和方法算出从A点出发到达B点,并禁止通过交叉点C的走法有多少种?
(3) 现由于交叉点C道路施工,禁止通行. 求如任选一种走法,从A点出发能顺利开车到达B点(无返回)概率是多少?