[重庆]2012届重庆万州区岩口复兴学校九年级下第一次月考数学试卷
如图, BD平分∠ABC, ED∥BC,若∠AED=50°,则∠D的度数等于( )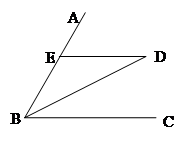
| A.50° | B.30° |
| C.40° | D.25° |
直线AB与直径6cm的⊙O相交, OD⊥AB于D,则OD的取值范围是( )
| A.OD>3 | B.OD<3 | C.0<OD<3 | D.OD=3 |
将图(1)所示的正六边形进行分割得到图(2),再将图(2)里的三个小正
六边形的其中之一按同样的方式进行分割得到图(3),接着再将图(3)中最小的三个正六边形的其中之一按同样的方式进行分割…,则第n 图形中共有( )个正六边形.
| A.3n | B.3n-2 | C.3n+2 | D.3(n-2) |
为加快把万州建成重庆市第二大都市,天城入城大道加紧施工。该工程全长6.1公里,路面铺设基本完成,目前已进入边坡治理及附属管道安装阶段。若其中某段工程共长1500米,在第6天工程完成一半时,因下雨停工两天,第三天恢复后加快了进度,工作效率是原来的 倍,正好按期完工。若用横轴表示工期,纵轴表示未完成的工程量,下面能反映这段工程的图像是( ).
倍,正好按期完工。若用横轴表示工期,纵轴表示未完成的工程量,下面能反映这段工程的图像是( ).
如图,在正方形ABCD的边长是2,点E是BC边的中点,过点B作BG⊥AE,垂足为G,延长BG交AC于点F,连结EF. 则下列结论中:①S△CEF:S△AFB=1:4;②AB=AF; ③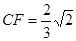 ;④S四边形ABEF=
;④S四边形ABEF=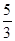 .正确的序号是( )
.正确的序号是( )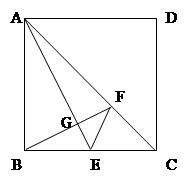
| A.①③ | B.①③④ |
| C.①②④ | D.②④ |
据重庆市2010年第六次全国人口普查公报:全市常住人口为2884.62万人,常住人口继续保持增长态势。这一数据用科学记数法表示为____________万人(结果保留两个有效数字).
在一次大课间体育锻炼时,某小组7位同学一分钟俯卧撑的个数分别是:25,30,27,18,27,25,31,27. 则这组数据的众数是_____________.
已知△ABC与△DEF相似且面积的比为4:9,则△ABC与△DEF的周长比为_____________.
已知⊙O的半径为6cm,直径CD⊥弦AB,点F在⊙O上,∠CFA=60°.则AB = ____ ___cm.
已知抛物线y=ax2+bx+1,从2,1中随机取一个值作为a,从1,0,-2中随机取一个值作为b,使该抛物线与x有公共点的概率是___________.
前年,某大型工业企业落户万州,相关建设随即展开.到去年年底,工程进入到设备安装阶段.在该企业的采购计划中,有A、B、C三种生产设备.若购进3套A,7套B,1套丙,需资金63万元;若购进4套A,10套B,1套丙,需资金84万元.现在打算同时购进A、B、C各10套,共需资金___________________万元.
尺规作图:学校决定在植物园内开辟一块梯形土地ABCD培植草皮(如图),AD∥BC.其中MN是园林里的一条主水管,点B、点C在MN上.如今要在BC上的P点接一条与BC垂直的水管 ,并在这条新接水管的某处安置喷淋器E,喷淋器位于草坪内,且到AB、BC的距离相等.请你运用尺规作图,在原图中帮助确定点E的位置.(要求:不写已知、求作及作法;保留作图痕迹)
如图,在正方形ABCD中,点G为BC上任意一点,连接AG,过B、
D两点分别作BE⊥AG,DF⊥AG,垂足分别为E、F两点.求证:AF=BE.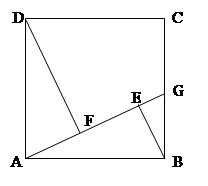
如图,已知直线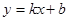 与x轴点A(-4,0),与y轴交于点B,与双曲线
与x轴点A(-4,0),与y轴交于点B,与双曲线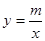 交于点C(a,3)和点D,且
交于点C(a,3)和点D,且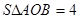 .
.
(1)求直线AB和双曲线的表达式;
(2)若CE⊥x轴于点E,连接DE.求⊿CDE的面积.
今年1月1日,欧盟强行推出了航空碳排放税,这一举措在国际航空业产生了极大反响,同时也说明解决环境问题刻不容缓。针对最普遍的汽车尾气排放,某中学一个课余环境研究小组在周末对部分私家车家庭上月出车天数进行调查后,制成了如下两幅不完整的统计图: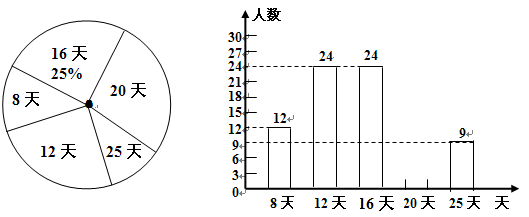
(1)参与调查的车主有 人,将条形统计图补充完整.
(2)若在出车25天的人,有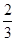 是生意人.专门调查这些生意人,发现其中男性驾驶员比女性驾驶员多2人,且有两人正好是来自同一家庭的夫妻.该小组决定从这几个生意人中任选两人进行为期三个月的连续调查,请用列表法或树状图,求出被选中的两人恰好是夫妻的概率.
是生意人.专门调查这些生意人,发现其中男性驾驶员比女性驾驶员多2人,且有两人正好是来自同一家庭的夫妻.该小组决定从这几个生意人中任选两人进行为期三个月的连续调查,请用列表法或树状图,求出被选中的两人恰好是夫妻的概率.
在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E. 
(1)求证:BE=DE;
(2)若四边形ABCD的面积为8,且tan∠A=3,求AB的长.
绿源无公害农产品公司生产的某种高端蔬菜每千克成本20元,经调查发现,这种蔬菜在未来40天内的日销量M(千克)与时间t(天)的关系如下表:
| 时间t(天) |
1 |
3 |
6 |
10 |
36 |
…… |
| 日销售量M(千克) |
94 |
90 |
84 |
76 |
24 |
…… |
未来40天内,前20天每天的价格y1(元/千克)与时间t(天)的函数关系为 (1≤t≤20,且t为整数),后20天每天的价格y2(元/千克)与时间t(天)的函数关系是
(1≤t≤20,且t为整数),后20天每天的价格y2(元/千克)与时间t(天)的函数关系是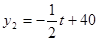 (21≤t≤40且t 为整数).
(21≤t≤40且t 为整数).
(1)分析上表,请用所学过的一次函数、二次函数、反比例函数的知识求出M(千克)与时间t(天)之间的函数关系式;
(2)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中,为推广促销,该公司决定每销售这种蔬菜1千克就给顾客返回a (a<4)元现金作为激励.公司通过销售记录发现,前20天中,每天扣除返回后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
已知:直角梯形AOBC在平面直角坐标系中的位置如图,若AC∥OB,OC平分∠AOB,CB⊥x轴于B,点A坐标为(3 ,4). 点P从原点O开始以2个单位/秒速度沿x轴正向运动 ;同时,一条平行于x轴的直线从AC开始以1个单位/秒速度竖直向下运动 ,交OA于点D,交OC于点M,交BC于点E. 当点P到达点B时,直线也随即停止运动. 
(1)求出点C的坐标;
(2)在这一运动过程中, 四边形OPEM是什么四边形?请说明理由。若
用y表示四边形OPEM的面积 ,直接写出y关于t的函数关系式及t的
范围;并求出当四边形OPEM的面积y的最大值?
(3)在整个运动过程中,是否存在某个t值,使⊿MPB为等腰三角形?
若有,请求出所有满足要求的t值.
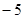
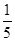
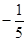
 ,自变量x的取值范围是( )
,自变量x的取值范围是( )




 的图像如图,正确的是( )
的图像如图,正确的是( )

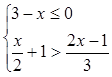
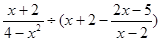 ,其中
,其中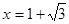 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号