初中数学一次函数的最值解答题

网络时代的到来，很多家庭都接入了网络，电信局规定了拨号入网两种收费方式，用户可以任选其一：A：计时制：0.05元／分；B：全月制：54元／月（限一部个人住宅电话入网）。此外B种上网方式要加收通信费0.02元／分。
①某用户某月上网的时间为x小时，两种收费方式的费用分别为（元）、（元），写出、与x之间的函数关系式。
②在上网时间相同的条件下，请你帮该用户选择哪种方式上网更省钱？

已知一次函数图象经过（3,　5）和（－4，－9）两点，①求此一次函数的解析式；
②若点（a，2）在函数图象上，求a的值。

某校八年级学生小丽、小强和小红到某超市参加了社会实践活动，在活动中他们参与了某种水果的销售工作，已知该种水果的进价为8元／千克，下面是他们在活动结束后的对话：
小丽：如果以10元／千克的价格销售，那么每天可售出300千克．
小强：如果以13元／千克的价格销售，那么每天可获取利润750元．
小红：通过调查验证，我发现每天的销售量（千克）与销售单价（元）之间存在一次函数关系．求（千克）与（元）（）的函数关系式；

若直线与两坐标轴围成的三角形面积为9，求的值。

已知y与x+2成正比例，当x=1时，y=-6，点（a，2）满足这个函数，求a.

已知一次函数的图像经过点A(1，0)和B（），且点B在反比例函数的图像上．
（1）求一次函数的解析式；
（2）若点M是轴上一点，且满足△ABM是直角三角形，请直接写出点M的坐标．

甲船从A港出发顺流匀速驶向B港，行至某处，发现船上一救生圈不知何时落入水中，立刻原路返回，找到救生圈后，继续顺流驶向B港．乙船从B港出发逆流匀速驶向A港．已知救生圈漂流的速度和水流速度相同；甲、乙两船在静水中的速度相同．甲、乙两船到A港的距离y₁、y₂（km）与行驶时间x（h）之间的函数图象如图所示．

（1）写出乙船在逆流中行驶的速度．
（2）求甲船在逆流中行驶的路程．
（3）求甲船到A港的距离y₁与行驶时间x之间的函数关系式．
（4）求救生圈落入水中时，甲船到A港的距离．
【参考公式：船顺流航行的速度船在静水中航行的速度＋水流速度，船逆流航行的速度船在静水中航行的速度水流速度．】

如图，直线AB与y轴交于点A,与x轴交于点B，点A的纵坐标、点B的横坐标如图所示．
（1）求直线AB的解析式；
（2）过原点O的直线把△ABO分成面积之比为2:1的两部分，请求出这条直线的解
析式．

如图，A、B分别表示一骑自行车者和一骑摩托车者在两城镇间旅行时路程与时间的关系，根据这个图像，你能得到关于这两个旅行者在旅行中的哪些信息？（至少写出6个）
                                    

已知一次函数y=kx+b（k≠0）图象过点（0，2），且与两坐标轴围成的三角形面积为2，求此一次函数的解析式．

如图，在平面直角坐标系中，一次函数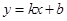的图象分别交x轴、y轴于A、B两点，与反比例函数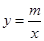的图象交于C、D两点，DE⊥x轴于点E。已知C点的坐标是(6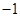，)，AE=6，tan∠DAE=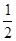

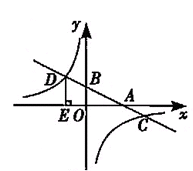
（1）求反比例函数与一次函数的解析式。
（2）根据图象直接回答：当x为何值时，一次函数的值大于反比例函数的值?

某医药研究所开发了一种新药，在试验药效时发现，如果成人按规定剂量服用，那么服药后2小时血液中含药量最高，达到每毫升6微克，接着就逐步衰减，10小时后血液中含药量为每毫升3微克，每毫升血液中含药量（微克）随时间（小时）的变化如图所示，那么成年人按规定剂量服药后：

（1）与之间的函数关系式．
（2）如果每毫升血液中含药量在4微克或4微克以上时，治疗疾病才是有效的，那么这个有效时间是多长?

图为一位旅行者在早晨８时从城市出发到郊外所走的路程S（单位：千米）与时间t（单位：时）的变量关系的图象。根据图象回答问题：

（1）在这个变化过程中，自变量是____，因变量是______。
（2）９时，１０时３０分，１２时所走的路程分别是多少？
（3）他休息了多长时间？
（4）他从休息后直至到达目的地这段时间的平均速度是多少？

将长为38cm，宽为5cm的长方形白纸，按如图所示方法粘合在一起，粘合部分白纸为2cm。

（1）求10张白纸粘合后的长度；
（2）设x张白纸粘合后的总长为ycm，写出y与x的函数关系式。

已知等腰三角形的周长为12，底边为y，腰长为x，求y与x的函数关系式，并求自变量x的取值范围