初中数学一次函数的最值解答题

湖州市八里店镇戴山村生产一种绿色蔬菜，直接销售每吨利润可达2000元；若经粗加工后再销售，每吨利润可达4500元；若经精加工后销售，每吨利润涨到7500元。
当地一家公司收获这种蔬菜140吨，该公司的生产能力是：如果蔬菜进行粗加工，每天可加工16吨；如果进行精加工，每天可加工6吨，但这两种加工方式不能同时进行，受季节条件限制公司必须用15天时间将这批蔬菜全部销售或加工完毕，该公司现有如下两种方案：
方案1：将蔬菜进行精加工，剩下的可直接销售；
方案2：将一部分蔬菜进行精加工，其余进行粗加工，并恰好用15天完成；
试通过分析运算，你认为选择哪种方案获利较多？

已知一次函数y=x+2
（1）在平面直角坐标系内画出函数y=x+2的图像 ；

（2）求当x=2时，y的值；

若△ABC中∠A＝60°，∠B的度数为x，∠C的度数为y，试写出y与x之间的函数关系式，并画出图象。

已知反比例函数和一次函数y=2x-1，其中一次函数的图像经过点（k，5）.
（1）求反比例函数的解析式；
（2）若点A在第一象限，且同时在上述两个函数的图象上，求A点的坐标。

年春季，我国云南、贵州等西南地区遇到多年不遇旱灾，“一方有难，八方支援”，为及时灌溉农田，丰收农机公司决定支援上坪村甲、乙、丙三种不同功率柴油发电机共10台（每种至少一台）配套相同型号抽水机4台、3台、2台，每台抽水机每小时可抽水灌溉农及田1亩.现要求所有柴油发电机及配套抽水机同时工作一小时，灌溉农田32亩.
(1)设甲种柴油发电机数量为x台，乙种柴油发电机数量为y台.
①用含x、y的式子表示丙种柴油发电机的数量；
②求出y与x的函数关系式；
(2)已知甲、乙、丙柴油发电机每台每小时费用分别为130元、120元、100元，应如何安排三种柴油发电机的数量，既能按要求抽水灌溉，同时柴油发电机总费用W最少？

已知⊙O₁经过，，，四点，一次函数的图象是直线，直线与轴交于点．

(1)在如图的平面直角坐标系中画出直线l，则直线与⊙O₁的交点坐标为      _______________   ；
(2)若⊙O₁上存在整点(横坐标与纵坐标均为整数的点称    
为整点)，使得为等腰三角形，所有满足条件的点的坐标为     _____________    ；
（3）将沿X轴向右平移            个单位时， 与y轴相切

如图，已知一次函数y=kx+b的图象经过点(0，4)和（1，6），

（1）求这个函数表达式并判断（－3，－2）是否在此函数的图象上；
（2）求该函数图像与x轴、y轴围成三角形的面积。

已知正比例函数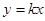的图象过点P（3，-3）。
（1）写出这个正比例函数的函数解析式；
（2）已知点 A(a，2)在这个正比例函数的图象上，求a的值。

已知一次函数y=kx+b的图像经过点（1，1），（-2，-5）.
（1）求此函数的解析式。
（2）若点（a，3）在此函数的图像上，求a的值为多少？

(1)小张自主创业开了一家服装店，因为进货时没有进行市场调查，在换季时积压了一批服装。为了缓解资金压力，小张决定打折销售。若每件服装按标价的5折出售将亏20元，而按标价的8折出售将赚40元。
①请你算一算每件服装的标价是多少元？
②为了尽快减少库存，又要保证不亏本，请你告诉小张最多能打几折。
(2)小张认真总结了前一次的教训，进行了详细的市场调查后第二次进货500件，按第一次的标价销售了300件后，剩下的进行甩卖，为了尽快减少库存，又要保证盈利两万元钱，请你告诉小张最多能打几折。

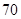（本小题7分）汽车由北京驶往相距千米的沈阳，汽车的速度是每小时千米，t小时后，汽车距沈阳s千米.
（1）求s与t的函数关系式，并写出自变量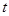的取值范围；
（2）经过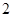小时后，汽车离沈阳多少千米？
（3）经过多少小时后，汽车离沈阳还有千米？

如图，平面直角坐标系中，点A（4，0），直线AB与y轴交于点B，S_△AOB=6，点P从点A出发，以每秒1个单位的速度沿x轴正方向运动．

求B点坐标。
过点B作射线L∥x轴，动点Q从B出发，以每秒2个单位的速度，沿射线L运动．若动点P、Q同时运动，过点A作AC⊥AB,射线AC与射线PQ、射线L分别交于点C、K．设运动时间为t秒，线段KQ的长为y个单位．求y与t的函数关系式，并直接写出自变量t的取值范围．
在（2）的条件下，若D为BC中点．在点P、Q运动过程中是否存在t值， 以A、C、D、Q为顶点的四边形是平行四边形，若存在，求出t值；若不存在，请说明理由．

（本题满分10分，其中第（1）4分、第（2）小题6分）
某公司销售一种商品，这种商品一天的销量y（件）与售价x（元/件）之间存在着如图所示的一次函数关系，且40≤x≤70．

（1）根据图像，求ｙ与x之间的函数解析式；
（2）设该销售公司一天销售这种商品的收入为w元．
①试用含x的代数式表示w；
②如果该商品的成本价为每件30元，试问当售价定为每件多少元时，该销售公司一天销售该商品的盈利为1万元？（收入=销量×售价）

阅读下面的材料：
在平面几何中，我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线，给出它们平行的定义：设一次函数y＝k₁x＋b₁（k₁≠0）的图象为直线l₁，一次函数y＝k₂x＋b₂（k₂≠0）的图象为直线l₂，若k₁＝k₂，且b₁≠b₂，我们就称直线l₁与直线l₂互相平行.

解答下面的问题：
（1）求过点P（1，4）且与已知直线y＝－2x－1平行的直线的函数表达式，并画出直线l的图象；
（2）设直线l分别与y轴、x轴交于点A、B，如果直线：y＝kx＋t ( t＞0)与直线l平行且交x轴于点C，求出△ABC的面积S关于t的函数表达式.

本题中的图象，是表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港，行驶过程中路程y（千米）随时间x（小时）变化的图象（分别是正比例函数图象和一次函数图象）．根据图象解答下列问题：

（1）分别求出表示轮船和快艇行驶过程中路程y（千米）随时间x（小时）变化的函数关系式（不要求写出自变量的取值范围）；
（2）轮船和快艇在途中行驶的速度分别是多少？
（3）快艇出发多长时间后追上轮船？