初中数学一次函数的最值解答题

直线经过点（3，5），求关于的不等式≥0的解集．

我市某林场计划购买甲、乙两种树苗共800株，甲种树苗每株24元，乙种树苗每株30元．相关资料表明：甲、乙两种树苗的成活率分别为85%，90%．
（1）若购买这两种树苗共用去21000元，则甲、乙两种树苗各购买多少株？
（2）若要使这批树苗的总成活率不低于88%，则甲种树苗至多购买多少株？
（3）在（2）的条件下，应如何选购树苗，使购买树苗的费用最低，并求出最低费用．

某公司到果品基地购买某种优质水果慰问医务工作者，果品基地对购买量在3000kg以上（含3000kg）的顾客采用两种销售方案。
甲方案：每千克9元，由基地送货上门；
乙方案：每千克8元，由顾客自己租车运回。
已知该公司租车从基地到公司的运输费用为5000元。
分别写出该公司两种购买方案付款金额y（元）与所购买的水果量x（kg）之间的关系式
⑵当购买量在哪一范围时，选择哪种购买方案付款最少？并说明理由。

小轿车从甲地出发驶往乙地，同时货车从相距乙地60km的入口处驶往甲地（两车均在甲、乙两地之间的公路上匀速行驶），下图是它们离甲地的路程y（km）与货车行驶时间x（h）之间的函数的部分图象．

（1）求货车离甲地的路程y（km）与它的行驶时间x（h）的函数关系式；
（2）哪一辆车先到达目的地？说明理由．

某学校计划购买若干台电脑，现从两家商场了解到同一型号电脑每台报价均为6000元，并且多买都有一定的优惠，甲商场的优惠方案是：第一台按原价收费，其余每台优惠25%；乙商场的优惠条件是：每台优惠20%．
（1）分别写出两家商场的收费（y）与所买电脑台数（x）之间的关系；
（2）什么情况下到两家商场购买，收费相同？
（3）什么情况下到甲商场购买更优惠？什么情况下到乙商场购买更优惠？

甲、乙两山地自行车选手进行骑行训练．他们在同地出发，反向而行，分别前往A地和B地．甲先出发一分钟且先到达A地．两人到达目的地后均以原速按原路立即返回，直至两人相遇．下图是两人之间的距离y（千米）随乙出发时间x（分钟）之间的变化图象．请根据图象解决下列问题：

（1）甲的速度为         千米/小时，乙的速度为         千米/小时；
（2）在图中的括号内填上正确的数值；
（3）乙出发多长时间两人首次相距22.6千米？

如图，在平面直角坐标系中，反比例函数的图象与一次函数的图象的一个交点为.

（1）求反比例函数的解析式；
（2）设一次函数的图象与轴交于点，若是轴上一点，且满足的面积是3，直接写出点的坐标．

2012年秋冬北方干旱，光明社区出现饮用水紧张，每天需从社区外调运饮用水120吨.现从甲、乙两水厂调运饮用水到社区供水点，甲厂每天最多可调出80吨，乙厂每天最多可调出90吨.从两水厂运水到光明社区供水点的路程和运费如下表：

	到光明社区供水点的路程（千米）	运费（元/吨千米）
甲厂	20	12
乙厂	14	15

（1）若某天调运水的总运费为26700元，则从甲、乙两水厂各调运了多少吨饮用水？
（2）设某天从甲厂调运饮用水吨，总运费为元，试写出关于的函数关系式，并求出这天运费最少为多少元？

黄岩岛是我国南沙群岛的一个小岛，渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后，发现一外国舰艇进入我国水域向黄岩岛驶来，渔船向渔政部门报告，并立即返航.渔政船接到报告后，立即从该港口出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t之间的函数图象.（假设渔船与渔政船沿同一航线航行）

(1)直接写出渔船离港口的距离s和它离开港口的时间t的函数关系式.
(2)求渔船和渔政船相遇时，两船与黄岩岛的距离.
(3)在渔政船驶往黄岩岛的过程中，求渔船从港口出发经过多长时间与渔政船相距30海里？

已知一次函数y＝kx＋b的图象经过点（－1，－4），且与正比例函数y＝x+1的图象相交于点（2，a），求
（1）a的值
（2）k，b的值
（3）这两个函数图象与x轴所围成的三角形面积.

近年来，我国煤矿安全事故频频发生，其中危害最大的是瓦斯，其主要成分是CO．在一次矿难事件的调查中发现：从零时起，井内空气中CO的浓度达到4mg/L，此后浓度呈直线型增加，在第7小时达到最高值46mg/L，发生爆炸；爆炸后，空气中的CO浓度成反比例下降．如图所示，根据题中相关信息回答下列问题：

（1）求爆炸前后空气中CO浓度y与时间x的函数关系式，并写出相应的自变量取值范围；
（2）当空气中的CO浓度达到34mg/L时，井下3km的矿工接到自动报警信号，这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生？
（3）矿工只有在空气中的CO浓度降到4mg/L及以下时，才能回到矿井开展生产自救，求矿工至少在爆炸后多少小时才能下井？

已知：一次函数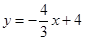的图象与x轴、y轴的交点分别为A、B，以B为旋转中心，将△BOA逆时针旋转，得△BCD（其中O与C、A与D是对应的顶点）.

（1）求AB的长；
（2）当∠BAD=45°时，求D点的坐标；
（3）当点C在线段AB上时，求直线BD的关系式.

4月20日8时2分，四川省雅安市芦山县发生了7.0级地震，当地的部分房屋严重受损，上万灾民无家可归，灾情牵动亿万中国人的心。某市积极筹集救灾物质 260吨物资从该市区运往雅安甲、乙两地，若用大、小两种货车共20辆，恰好能一次性运完这批物资。已知这两种货车的载重量分别为16吨/辆和10吨/辆，运往甲、乙两地的运费如下表：

车 型 运往地	甲 地（元/辆）	乙 地（元/辆）
大货车	720	800
小货车	500	650

（1）求这两种货车各用多少辆？
（2）如果安排9辆货车前往甲地，其余货车前往乙地，设前往甲地的大货车为辆，前往甲、乙两地的总运费为w元，求出w与的函数关系式（写出自变量的取值范围）；
（3）在（2）的条件下，若运往甲地的物资不少于132吨，请你设计出使总运费最少的货车调配方案，并求出最少总运费

如图，已知A(-4,n)，B(1,-4)是一次函数的图象和反比例函数的图象的两个交点．

(1)求反比例函数和一次函数的解析式；
(2)求直线与轴的交点的坐标及△的面积；
(3)求不等式的解集（请直接写出答案）.

如图，一次函数的图象与反比例函数（x＜0）的图象相交于A点，与y轴、x轴分别相交于B、C两点，且C（2，0），A点的横坐标为-1.

（1）求一次函数的解析式；
（2）设函数（x＞0）的图象与（x＜0）的图象关于y轴对称，在（x＞0）的图象上取一点P（P点的横坐标大于2），过P点作PQ⊥x轴，垂足是Q，若四边形BCQP的面积等于2，求P点的坐标．