[山东]2013届山东省潍坊市九年级学业水平模拟考试(二模)数学试卷.
关于 的一元二次方程
的一元二次方程 有一个根等于 -1,则另一个根等于( )
有一个根等于 -1,则另一个根等于( )
| A.-2 | B.1 | C.2 | D.3 |
数学课要学“勾股定理”,小敏在“百度”搜索引擎中输入“勾股定理”,能搜索到与之相关的结果个数 约为7160 000,这个数用科学记数法表示为( )
| A.7.16×105 | B.7.16×106 | C.7.16×107 | D.7.16×108 |
右图是由4个相同的小正方体组成的几何体,其俯视图为( )




(A) (B) (C) (D)
如图,在等腰Rt△ABC中,∠C=90o,AC=6,D是AC上一点,若tan∠DBC= ,则AD的长为( )
,则AD的长为( )
| A.2 | B.4 | C. |
D. |
在△ABC中,若三边BC ,CA,AB满足 BC:CA:AB=5:12:13,则cosB=( )
A. |
B. |
C. |
D. |
某医院决定抽调甲、乙、丙、丁4名医护人员参加抗震救灾,先随机地从这4人中抽取2人作为第一批救灾医护人员,那么丁医护人员被抽到作为第一批救灾医护人员的概率是( )
A. |
B. |
C. |
D. |
已知点P是半径为5 的⊙O内的一点,且OP=3,则过点P的所有⊙O的弦中,最短的弦长等于( ).
| A.4 | B.6 | C.8 | D.10 |
如图,直线 过点A(0,2),且与直线
过点A(0,2),且与直线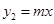 交于点P(1,m),则不等式组
交于点P(1,m),则不等式组 的解是( )
的解是( )
A.1< <2 <2 |
B.0< <2 <2 |
C.0< <1 <1 |
D.1< |
点P是矩形ABCD的边AD上的一个动点,矩形的两条边AB、AC的
长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是
A. B.
B. C.
C. D.不确定
D.不确定
如图:点A在双曲线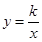 上,AB⊥x轴于B,且△AOB的面积S△AOB=2,则k=______.
上,AB⊥x轴于B,且△AOB的面积S△AOB=2,则k=______.
在直角坐标平面上,横坐标与纵坐标都是整数的点称为整点.如果将二次函数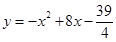 与
与 轴所围成的封闭图形染成红色,则在此红色内部区域及其边界上的
轴所围成的封闭图形染成红色,则在此红色内部区域及其边界上的
整点个数是 .
某市今年的信息技术结业考试,采用学生抽签的方式决定自己的考试内容。规定:每位考生先在三个笔试题(题签分别用代码 表示)中抽取一个,再在三个上机题(题签分别用代码
表示)中抽取一个,再在三个上机题(题签分别用代码 表示)中抽取一个进行考试。小亮在看不到题签的情况下,分别从笔试题和上机题中随机地各抽取一个题签。
表示)中抽取一个进行考试。小亮在看不到题签的情况下,分别从笔试题和上机题中随机地各抽取一个题签。
(1)用树状图或列表法表示出所有可能的结构;
(2)求小亮抽到的笔试题和上机题的题签代码的下标(例如“ ”的下表为“1”)均为奇数的概率。
”的下表为“1”)均为奇数的概率。
如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.
(1)求证:AD=EC;
(2)当∠BAC= 时,求证:四边形ADCE是菱形.
时,求证:四边形ADCE是菱形.
我市某林场计划购买甲、乙两种树苗共800株,甲种树苗每株24元,乙种树苗每株30元.相关资料表明:甲、乙两种树苗的成活率分别为85%,90%.
(1)若购买这两种树苗共用去21000元,则甲、乙两种树苗各购买多少株?
(2)若要使这批树苗的总成活率不低于88%,则甲种树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低,并求出最低费用.
如图,AB是⊙O的直径,弦CE⊥AB交AB于点D,点P在AB的延长线上, 连结OE、AC、BC,已知∠POE=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)若BD=2OD,且PB=12,求⊙O的半径.
某中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为50米的篱笆围成。已知墙长为26米(如图所示),设这个苗圃园平行于墙的一边的长为 米。(1)若垂直于墙的一边长为
米。(1)若垂直于墙的一边长为 米,直接写出
米,直接写出 与
与 的函数关系式及其自变量
的函数关系式及其自变量 的取值范围;(2)当
的取值范围;(2)当 为多少米时,这个苗圃园的面积最大,并求出这个最大值;(3)当这个苗圃园的面积不小于300平方米时,试结合函数图象,求出
为多少米时,这个苗圃园的面积最大,并求出这个最大值;(3)当这个苗圃园的面积不小于300平方米时,试结合函数图象,求出 的取值范围。
的取值范围。




 的平方根是( )
的平方根是( )


 的值为0,则
的值为0,则 的值等于( )
的值等于( )
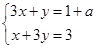 的解满足
的解满足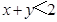 ,则a的取值范围为______.
,则a的取值范围为______.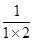 =1-
=1-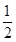 ;
; 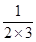 =
=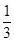 ;
;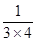 =
= ;……则
;……则 _____.
_____.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号