如图，△ABC中，AD是边BC上的中线，过点A作AE∥BC，过点D作DE∥AB，DE与AC、AE分别交于点O、点E，连接EC．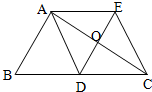
（1）求证：AD=EC；
（2）当∠BAC=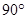
时，求证：四边形ADCE是菱形．
，
，
，
．
，
，
．
与
；
与
．
．
相关知识点
推荐套卷
如图，△ABC中，AD是边BC上的中线，过点A作AE∥BC，过点D作DE∥AB，DE与AC、AE分别交于点O、点E，连接EC．
（1）求证：AD=EC；
（2）当∠BAC=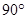时，求证：四边形ADCE是菱形．
粤公网安备 44130202000953号