[江苏]2013届江苏省南京市白下区中考二模数学试卷
某病毒长度约为0.000058 mm,将0.000058用科学记数法表示为
| A.5.8×10-6 | B.5.8×10-5 | C.0.58×10-5 | D.58×10-6 |
从标号分别为1,2,3,4,5的5张卡片中,随机抽取1张,下列事件中,必然事件是
| A.该卡片标号小于6 | B.该卡片标号大于6 |
| C.该卡片标号是奇数 | D.该卡片标号是3 |
如图,数轴上有O、A、B、C、D五点,根据图中各点所表示的数,判断3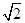 在数轴上对应的点的位置是
在数轴上对应的点的位置是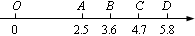
A.在线段OA上 B.在线段AB上
C.在线段BC上 D.在线段CD上
快车和慢车同时从A地出发,分别以速度v1、v2(v1>2v2)匀速向B地行驶,快车到达B地后停留了一段时间,沿原路仍以速度v1匀速返回,在返回途中与慢车相遇.在上述过程中,两车之间的距离y与慢车行驶时间x之间的函数图象大致是
甲、乙两名学生在某次打靶游戏中各射击4次,两人的测试成绩如下(单位:环):
甲 6 7 8 9
乙 6.5 6.5 8.5 8.5
则测试成绩比较稳定的是 (填“甲”或“乙”).
用平行四边形的定义和课本上的三个定理可以判断一个四边形是平行四边形,请探索并写出一个与它们不同的平行四边形的判定方法: .
在梯形ABCD中,AD∥BC,∠B=90°,AD=2cm,AB=8cm,E是AB上一点,连接DE、CE.若满足∠DEC=90°的点E有且只有一个,则BC= cm.
从甲地到乙地有A1、A2两条路线,从乙地到丙地有B1、B2、B3三条路线,其中A1B2是从甲地到丙地的最短路线.一个人任意选了一条从甲地到丙地的路线,他恰好选到最短路线的概率是多少?
飞机测量一岛屿两端A、B的距离,在距海平面垂直高度为200m的点C处测得A的俯角为53°,然后沿着平行于AB的方向水平飞行了300m,在点D处测得B的俯角为45°,求岛屿两端A、B的距离.(参考数据:sin53°≈ ,cos53°≈
,cos53°≈ ,tan53°≈
,tan53°≈ )
)
D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC平面上的一动点,连接OB、OC,G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
(1)如图,当点O在△ABC内时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,点O所在位置应满足什么条件?(直接写出答案,不需说明理由.)
某校九年级男生进行引体向上训练,体育老师随机选择了部分男生,根据训练前成绩编组:0~4个的编为第一组,5~8个的编为第二组,9~12个的编为第三组,在训练后制作了如下两幅统计图,请回答下列问题:
(1)下列说法正确的是 (填写所有正确的序号).
①训练后,第一组引体向上平均成绩的增长率最大;
②训练前,所选男生引体向上成绩的中位数一定在第二组;
③训练前,所选男生引体向上成绩的众数一定在第二组.
(2)估计该校九年级全体男生训练后的平均成绩是多少?
小轿车从甲地出发驶往乙地,同时货车从相距乙地60km的入口处驶往甲地(两车均在甲、乙两地之间的公路上匀速行驶),下图是它们离甲地的路程y(km)与货车行驶时间x(h)之间的函数的部分图象.
(1)求货车离甲地的路程y(km)与它的行驶时间x(h)的函数关系式;
(2)哪一辆车先到达目的地?说明理由.
如图,在△ABC中,∠A=∠B=30°,过点C作CD⊥AC,交AB于点D.
(1)作⊙O,使⊙O经过A、C、D三点(尺规作图,保留作图痕迹,不写作法);
(2)判断直线 BC与⊙O的位置关系,并说明理由.
问题:已知线段AB、CD相交于点O,AB=CD.连接AD、BC,请添加一个条件,使得△AOD≌△COB.
小明的做法及思路
小明添加了条件:∠DAB=∠BCD.他的思路是:分两种情况画图①、图②,在两幅图中,
都作直线DA、BC,两直线交于点E.
由∠DAB=∠BCD,可得∠EAB=∠ECD.
∵AB=CD,∠E=∠E,
∴△EAB≌△ECD.∴EB=ED,EA=EC.
图①中ED-EA=EB-EC,即AD=CB.
图②中EA-ED=EC-EB,即AD=CB.
又∵∠DAB=∠BCD,∠AOD=∠COB,
∴△AOD≌△COB.
数学老师的观点:
(1)数学老师说:小明添加的条件是错误的,请你给出解释.
你的想法:
(2)请你重新添加一个满足问题要求的条件
,并说明理由.
某汽车销售公司10月份销售某厂家的汽车.在一定范围内,每部汽车的进价与销售量有如下关系:若当月仅售出1部汽车,则该部汽车的进价为30万元;每多售出1部,所有售出的汽车的进价均降低0.2万元/部.
(1)若该公司当月售出2部汽车,则每部汽车的进价为 万元;
(2)如果汽车的售价为31万元/部.
①写出公司当月盈利y(万元)与汽车销售量x(部)之间的函数关系式;
②若该公司当月盈利28万元,求售出汽车的数量.
(1)如图①,P为△ABC的边AB上一点(P不与点A、点B重合),连接PC,如果△CBP∽△ABC,那么就称P为△ABC的边AB上的相似点.
画法初探
①如图②,在△ABC中,∠ACB>90°,画出△ABC的边AB上的相似点P(画图工具不限,保留画图痕迹或有必要的说明);
辩证思考
②是不是所有的三角形都存在它的边上的相似点?如果是,请说明理由;如果不是,请找出一个不存在边上相似点的三角形;
特例分析
③已知P为△ABC的边AB上的相似点,连接PC,若△ACP∽△ABC,则△ABC的形状是 ;
④如图③,在△ABC中,AB=AC,∠A=36°,P是边AB上的相似点,求的值.
(2)在矩形ABCD中,AB=a,BC=b(a≥b).P是AB上的点(P不与点A、点B重合),作PQ⊥CD,垂足为Q.如果矩形ADQP∽矩形ABCD,那么就称PQ为矩形ABCD的边AB、CD上的相似线.
①类比(1)中的“画法初探”,可以提出问题:对于如图④的矩形ABCD,在不限制画图工具的前提下,如何画出它的边AB、CD上的相似线PQ呢?
你的解答是: (只需描述PQ的画法,不需在图上画出PQ).
②请继续类比(1)中的“辩证思考”、“特例分析”两个栏目对矩形的相似线进行研究,要求每个栏目提出一个问题并解决.
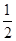
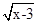 在实数范围内有意义,则x的取值范围是 .
在实数范围内有意义,则x的取值范围是 .
 ,OC=1,则OB的长为 .
,OC=1,则OB的长为 .
 的图象经过点(1,1),那么它还经过(-2, ).
的图象经过点(1,1),那么它还经过(-2, ). +(
+( )-1+(2-π)0-(
)-1+(2-π)0-( )2.
)2. ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
 -
- =0.
=0. 粤公网安备 44130202000953号
粤公网安备 44130202000953号