D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC平面上的一动点,连接OB、OC,G、F分别是OB、OC的中点,顺次连接点D、G、F、E.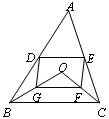
(1)如图,当点O在△ABC内时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,点O所在位置应满足什么条件?(直接写出答案,不需说明理由.)
相关知识点
推荐套卷
D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC平面上的一动点,连接OB、OC,G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
(1)如图,当点O在△ABC内时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,点O所在位置应满足什么条件?(直接写出答案,不需说明理由.)