（1）如图①，P为△ABC的边AB上一点（P不与点A、点B重合），连接PC，如果△CBP∽△ABC，那么就称P为△ABC的边AB上的相似点．
画法初探
①如图②，在△ABC中，∠ACB＞90°，画出△ABC的边AB上的相似点P（画图工具不限，保留画图痕迹或有必要的说明）；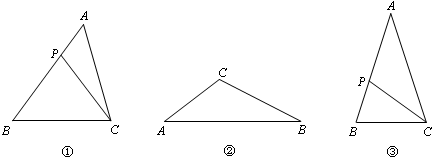
辩证思考
②是不是所有的三角形都存在它的边上的相似点？如果是，请说明理由；如果不是，请找出一个不存在边上相似点的三角形；
特例分析
③已知P为△ABC的边AB上的相似点，连接PC，若△ACP∽△ABC，则△ABC的形状是 ；
④如图③，在△ABC中，AB＝AC，∠A＝36°，P是边AB上的相似点，求的值．
（2）在矩形ABCD中，AB＝a，BC＝b（a≥b）．P是AB上的点（P不与点A、点B重合），作PQ⊥CD，垂足为Q．如果矩形ADQP∽矩形ABCD，那么就称PQ为矩形ABCD的边AB、CD上的相似线．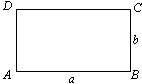
①类比（1）中的“画法初探”，可以提出问题：对于如图④的矩形ABCD，在不限制画图工具的前提下，如何画出它的边AB、CD上的相似线PQ呢？
你的解答是： （只需描述PQ的画法，不需在图上画出PQ）．
②请继续类比（1）中的“辩证思考”、“特例分析”两个栏目对矩形的相似线进行研究，要求每个栏目提出一个问题并解决．
（钦州）如图，AB为⊙O的直径，AD为弦，∠DBC=∠A．
（1）求证：BC是⊙O的切线；
（2）连接OC，如果OC恰好经过弦BD的中点E，且tanC=
，AD=3，求直径AB的长．
（柳州）如图，已知抛物线
的顶点坐标为M，与x轴相交于A，B两点（点B在点A的右侧），与y轴相交于点C．
（1）用配方法将抛物线的解析式化为顶点式：
（
），并指出顶点M的坐标；
（2）在抛物线的对称轴上找点R，使得CR+AR的值最小，并求出其最小值和点R的坐标；
（3）以AB为直径作⊙N交抛物线于点P（点P在对称轴的左侧），求证：直线MP是⊙N的切线．
（柳州）如图，已知四边形ABCD是平行四边形，AD与△ABC的外接圆⊙O恰好相切于点A，边CD与⊙O相交于点E，连接AE，BE．
（1）求证：AB=AC；
（2）若过点A作AH⊥BE于H，求证：BH=CE+EH．
（南宁）如图，AB是⊙O的直径，C，G是⊙O上两点，且AC=CG，过点C的直线CD⊥BG于点D，交BA的延长线于点E，连接BC，交OD于点F．
（1）求证：CD是⊙O的切线．
（2）若
，求∠E的度数．
（3）连接AD，在（2）的条件下，若CD=
，求AD的长．
粤公网安备 44130202000953号