初中数学一次函数的最值解答题

已知一次函数y＝kx＋b的图象经过点（0，4）与点（1，2）．
（1）求一次函数的解析式；
（2）若一次函数y＝kx＋b的图象还经过点（－1，m）与点（3，n），试比较m，n的大小．

已知一次函数y＝kx＋b的图像经过点（－1，－5），且与正比例函数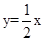的图像相交于点（2，m）.
求:（1）m的值；（2）一次函数y＝kx＋b的解析式；

已知y–3与x成正比例，当x=1时y=2.
（1）写出y与x之间的函数关系式
（2）求x=–1时，y的值

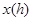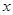一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为，两车之间的距离为，图中的折线表示与之间的函数关系．
根据图象进行以下探究

（1）请解释图中点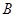的实际意义；
（2）求慢车和快车的速度；
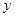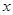（3）求线段BC所表示的与之间的函数关系式，并写出自变量的取值范围；

如图，直线：y=3x+1与直线：y=mx+n相交于点P（1，b）．

（1）求b的值；
（2）不解关于x，y的方程组请你直接写出它的解；
（3）直线：y=nx+m是否也经过点P？请说明理由．

(8分)如图，一直线BC与已知直线AB：关于y轴对称。

（1）求直线BC的解析式；
（2）说明两直线与x轴围成的三角形是等腰三角形。

某公司准备与汽车租赁公司签订租车合同。以每月用车路程x(km)计算，甲汽车租赁公司的月租费元，乙汽车租赁公司的月租费是元。如果、与x之间的关系如图所示。

（1）求、与x之间的函数关系
（2）每月用车路程在什么范围内，租用甲汽车租赁公司的车所需费用较少？

已知点A（0,0）、B（3,0），点C在y轴上，且△ABC的面积为5，求点C的坐标。

已知正比例函数的图象过点P（3，-3）。
（1）写出这个正比例函数的函数解析式；
（2）已知点 A(a，2)在这个正比例函数的图象上，求a的值。

某游泳馆的游泳池长50米，甲、乙二人分别在游泳池相对的A、B两边同时向另一边游去，其中s表示与A边的距离，t表示游泳时间，如图，l₁，l₂分别表示甲、乙两人的s与t的关系.

(1)l₁表示谁到A边的距离s与游泳时间t的关系；
(2)甲、乙哪个速度快？
(3)游泳多长时间，两人相遇？
(4) t＝30秒时，两人相距多少米？

某长途汽车站规定，乘客可以免费携带一定质量的行李，若超过该质量则需购买行李票，且行李票（元）与行李质量（千克）之间的一次函数关系式为，现知贝贝带了60千克的行李，交了行李费5元。
（1）若京京带了84千克的行李，则该交行李费多少元？
（2）旅客最多可免费携带多少千克的行李？

如图，在平面直角坐标系中，，，点Q从点A出发以1cm/s的速度向点B运动，点P从点O出发以2cm/s的速度在线段OC间往返运动，P、Q两点同时出发，当点Q到达点B时，两点同时停止运动.

（1）当运动秒时，=____________，的坐标是( ____  ,  ____ )(用含t的代数式表示)
（2）当t为何值时，四边形的面积为36cm²？
（3）当t为何值时，四边形为平行四边形？
（4）当t为何值时，四边形为等腰梯形？

在平面直角坐标系中，点P从原点O出发，每次向上平移2个单位长度或向右平移1个单位长度.

P从点O出发 平移次数	可能到达的 点的坐标
1 次	（0,2）（1,0）
2 次
3 次

实验操作
在平面直角坐标系中描出点P从点O出发，平移1次后，2次后，3次后可能到达的点，并把相应点的坐标填写在表格中.
观察思考
任一次平移，点P可能到达的点在我们学过的一次函数的图像上，如：平移1次后点P在函数________________的图像上；平移2次后点P在函数_________________的图像上
（3）规律发现
由此我们知道，平移n次后点P在函数__________________的图像上（请填写相应的解析式）

世界上大部分国家都使用摄氏（℃）温度，但美、英等国的天气预报仍然使用华氏（℉）温度，两种计量之间有如下对应：

℃	0	10	20	30
℉	32	50	68	86

（1）设摄氏温度为（℃）,华氏温度为（℉）,如果这两种计量之间的关系是一次函数，请求出该一次函数表达式.
（2）求出华氏0度时摄氏是多少度.
（3）华氏温度的值与对应的摄氏温度的值有相等的可能吗？请说明理由.

已知直线，它们能交于同一点吗？为什么？