[江苏]2011-2012学年江苏泰州市海陵区八年级上期末考试数学试卷
在平面直角坐标系中,点P(-3,2)在 ( ▲ )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
如图是小刚画的一张脸,他对妹妹说“如果我用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成 ( ▲ )
| A.(1,0) | B.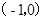 |
C. |
D.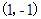 |
如图,杨伯家小院子的四棵小树 刚好在其梯形院子
刚好在其梯形院子 各边的中点上,若在四边形
各边的中点上,若在四边形 种上小草,则这块草地的形状是 ( ▲ )
种上小草,则这块草地的形状是 ( ▲ ) 
| A.平行四边形 | B.矩形 | C.正方形 | D.菱形 |
为筹备元旦联欢晚会,在准备工作中,班长对全班同学爱吃什么水果作了民意调查,再决定最终买哪种水果,下面的调查数据中,他会最关注 ( ▲ )
| A.众数 | B.平均数 | C.中位数 | D.加权平均数 |
下列说法不正确的是 ( ▲ )
| A.一组邻边相等的矩形是正方形 | B.对角线相等的菱形是正方形 |
| C.对角线互相垂直的矩形是正方形 | D.有一个角是直角的平行四边形是正方形 |
小明的父亲饭后出去散步,从家中走20分钟到一个离家900米的报亭看10分钟报纸后,用15分钟返回家里。下面图形中表示小明的父亲离家的时间与距离之间的关系是 ( ▲ ) 
海陵区2011年实现生产总值(GDP)2645亿元,用科学记数法表示应是____ ___亿元.(结果保留3个有效数字)
如图,□ABCD中, ∠B=110°,延长AD至F,延长CD至E,连接EF,则∠E+∠F= _________°。
如图1,平行四边形纸片 的面积为120,
的面积为120, ,
, .沿两对角线将四边形
.沿两对角线将四边形 剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(
剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并( 、
、 重合)形成对称图形戊,如图2所示,则图形戊的两条对角线长度之和是 。
重合)形成对称图形戊,如图2所示,则图形戊的两条对角线长度之和是 。
已知 与
与 成正比例函数关系,且
成正比例函数关系,且 时,
时, 。
。
(1)写出 与
与 之间的函数关系式;
之间的函数关系式;
(2)求当 时,
时, 的值;
的值;
(3)求当 时,
时, 的值。
的值。
在小正方形组成的15×15的网络中,四边形ABCD和四边形 的位置如图所示。
的位置如图所示。
⑴现把四边形ABCD绕D点按顺时针方向旋转900,画出相应的图形 ;
;
⑵若四边形ABCD平移后,与四边形 成轴对称,写出满足要求的一种平移方法,并画出平移后的图形
成轴对称,写出满足要求的一种平移方法,并画出平移后的图形 .
.
如图,已知AB=AC,DE垂直平分AB交AC、AB于E、D两点,若AB=12cm,BC=10cm,∠A=50o,求△BCE的周长和∠EBC的度数.
梯形ABCD中,AD∥BC,BD平分∠ABC,AE∥DC
试说明:⑴AE =" DC" ⑵ AB = CE
如图,若在象棋盘上建立直角坐标系,使“帥”位于点(-2,-3),“馬”位于点(1,-3),
(1)画出所建立的平面直角坐标系;
(2)分别写出“兵”和“炮”两点位于你所建立的平面直角坐标系的坐标。
为了普及环保知识,增强环保意识,某中学组织了环保知识竞赛活动,初中三个年级根据初赛成绩分别选出了10名同学参加决赛,这些选手的决赛成绩(满分为100分)如下表所示:
| |
决赛成绩(单位:分) |
| 初一年级 |
80 86 88 80 88 99 80 74 91 89 |
| 初二年级 |
85 85 87 97 85 76 88 77 87 88 |
| 初三年级 |
82 80 78 78 81 96 97 88 89 86 |
(1)请你填写下表:
| |
平均分 |
众数 |
中位数 |
| 初一年级 |
85.5 |
|
87 |
| 初二年级 |
85.5 |
85 |
|
| 初三年级 |
|
|
84 |
(2)请从以下两个不同的角度对三个年级的决赛成绩进行分析:
①从众数和平均数相结合看(分析哪个年级成绩好些);
②从平均数和中位数相结合看(分析哪个年级成绩好些)。
(3)如果在每个年级参加决赛的选手中分别选出3人参加总决赛,你认为哪个年级的实力更强些?并说明理由。
某公司每月付给销售人员的工资有两种方案.
方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成(注:销售提成是指从销售每件商品得到的销售额中提取一定数量的费用).
设销售商品的数量 (件),销售人员的月工资
(件),销售人员的月工资 (元).如图所示,
(元).如图所示, 为方案一的函数图象,
为方案一的函数图象, 为方案二的函数图象.从图中信息解答如下问题:
为方案二的函数图象.从图中信息解答如下问题:
(1)求 、
、 与x的函数关系式;
与x的函数关系式;
(2)请问方案二中每月付给销售人员的底薪是多少元?
(3)如果该公司销售人员小丽当月的月工资要为1800元,那么你认为小丽选用哪种方案销售件数少些?销售件数为多少?

 无理数的个数( ▲)
无理数的个数( ▲) 4
4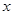 ,7的平均数6,则
,7的平均数6,则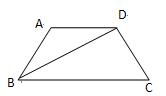
 是关于x的一次函数,且y随x的增大而增大,则m =___ _。
是关于x的一次函数,且y随x的增大而增大,则m =___ _。 的解是
的解是 

 和
和 ,求
,求 的值。
的值。 .
. 中,
中, 厘米,
厘米, 厘米,点
厘米,点 为
为 的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
 与
与 是否全等,请说明理由;
是否全等,请说明理由; 粤公网安备 44130202000953号
粤公网安备 44130202000953号