[贵州]2011-2012学年贵州省桐梓县八年级上学期期末考试数学试卷
下列各式是完全平方式的是( )
A.x2-x+ |
B.1+x2 | C.x+xy+l | D.x2+2a-l |
函数y=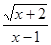 中自变量x的取值范围是( )
中自变量x的取值范围是( )
| A.x≥2 | B.x≠1 | C.x>-2且x≠1 | D.x≥-2且x≠1 |
等腰三角形一边长等于5,一边长等于9,则它的周长是( )
| A.14 | B.23 | C.19或23 | D.19 |
满足下列哪种条件时,能判定△ABC与△DEF全等的是 ( )
| A.∠A=∠E,AB=EF,∠B=∠D; | B.AB=DE,BC=EF,∠C=∠F; |
| C.AB=DE,BC=EF,∠A=∠E; | D.∠A=∠D,AB=DE,∠B=∠E |
直线y=-2x+a经过(3,y1,)和(-2,y2),则y1与y2的大小关系是( )
| A.y1> y2 | B.y1< y2 | C.y1= y2 | D.无法确定 |
如图,已知∠ABC=∠DEF,AB=DE,要说明△ABC≌△DEF,若以“SAS”为依据,还要添加的
一个条件为 .(B、E、C、F共线)
如图,已知函数y=2x+b和y=ax-3的图像交于点P(―2,―5),则根据图像可得不等式2x+b>ax-3的解集是 .
用“ ”与“
”与“ ”表示一种运算法则:(a
”表示一种运算法则:(a b)=-b,(a
b)=-b,(a b)=-a,如(2
b)=-a,如(2 3)=-3,则((2010
3)=-3,则((2010 2011)
2011) (2009
(2009 2008))= .(括号运算优先)
2008))= .(括号运算优先)
已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE。
求证:(1)△ABC≌△DEF;
(2)GF=GC。
如图,一次函数y=kx+b的图像经过A、B两点,与x轴相交于点C。
求:(1)此一次函数的解析式。
(2)△AOC的面积。
如图,在平面直角坐标系中,函数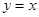 的图象
的图象 是第一、三象限的角平分线.
是第一、三象限的角平分线.
实验与探究:由图观察易知A(0,2)关于直线 的对称点
的对称点 的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5) 关于直线
的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5) 关于直线 的对称点
的对称点 、
、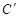 的位置,并写出它们的坐标:
的位置,并写出它们的坐标: 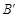 、
、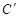 ;
;
归纳与发现:结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(m,n)关于第一、三象限的角平分线 的对称点
的对称点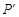 的坐标为 ;
的坐标为 ;
运用与拓广:已知两点D(0,-3)、E(-1,-4),试在直线 上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.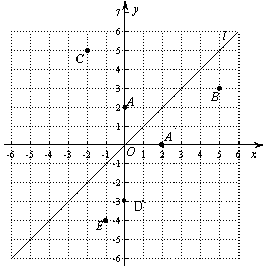
 ,4
,4 ,
, ,
, ,
, 中是无理数的有( ).
中是无理数的有( ).








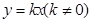 的函数值
的函数值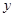 随
随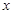 的增大而减小,则一次函数
的增大而减小,则一次函数 的图象大致是( ).
的图象大致是( ).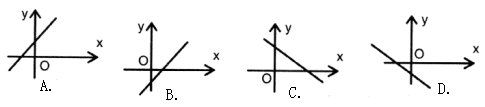
 = .
= . 向上平移2 个单位后的直线解析式 .
向上平移2 个单位后的直线解析式 . =3,则a2+
=3,则a2+ 的值是______________.
的值是______________.

 (
( )2+20110
)2+20110

 ,其中
,其中 ;
; 的平方根是
的平方根是 ,
, 的算术平方根是4,求
的算术平方根是4,求 的平方根。
的平方根。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号