小虎一家利用元旦三天驾车到某景点旅游,小汽车出发前油箱有油36L,匀速行驶若干小时后,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图象回答下列问题:
(1)求油箱余油量Q与行驶时间t之间的函数关系式;
(2)如果出发地距景点200km,车速为80km/h,要到达景点,油箱中的油是否够用?请说明理由.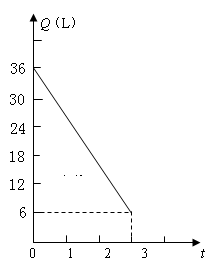
相关知识点
推荐套卷
小虎一家利用元旦三天驾车到某景点旅游,小汽车出发前油箱有油36L,匀速行驶若干小时后,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图象回答下列问题:
(1)求油箱余油量Q与行驶时间t之间的函数关系式;
(2)如果出发地距景点200km,车速为80km/h,要到达景点,油箱中的油是否够用?请说明理由.