[江苏]2011~2012学年江苏省姜堰八年级上学期期末联考数学试卷
△ABC中,D、E分别为AB、AC边的中点,若BC=8cm,则DE为
A.16cm B.8cm C.4cm D.2cm
如图,小手盖住的点的坐标可能为( )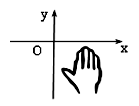
| A.(5,2) | B.(-6,3) | C.(-4,-6) | D.(3,-4) |
某班7名同学的一次体育测试成绩(满分30分)依次为:22,23,24,23, 22,23,25,这组数据的众数是
| A.22 | B.23 | C.24 | D.25 . |
Rt△ABC中,∠C=90°,AB=10,BC=8,AC的长度为
| A.6 | B.8 | C.10 | D.12 |
一次函数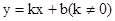 的图像如图所示,则
的图像如图所示,则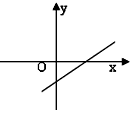
| A.k>0,b>0 | B.k>0,b<0 | C.k<0,b>0 | D.k<0,b<0 |
如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为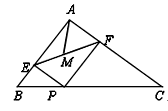
| A.2 | B.2.4 | C.2.6 | D.3 |
如图,在△ABC中,∠C=90º,∠ABC的平分线BD交AC于点D.若CD=8cm,则点D到直线AB的距离是 cm.
如图矩形ABCD中,对角线AC、BD相交于点O,若AB=1,∠AOB=60°,则BC=___________.
在空中,自地面算起,每升高1千米,气温下降若干度(℃).某地空中气温t(℃)与高度h(千米)间的函数的图像如图所示,那么当高度h= 千米时,气温为6(℃).
如图,已知A1(1,0),A2(1,-1),A3(-1,-1),A4(-1,1),A5(2,1),…,则点A2012的坐标是__________________.
如图,AC是菱形ABCD的对角线,点E、F分别在边AB、AD上,且AE=AF.试说明△ACE≌△ACF.
已知,一次函数 和
和 的图像交于点A(-1,m)
的图像交于点A(-1,m)
⑴求出m,b的值;
⑵求出这两条直线与x轴围成的图形的面积。
某海港某日0时到24时的水深 与时间
与时间 的变化关系如图1所示:
的变化关系如图1所示:
⑴水深何时最小?最小水深为多少?
⑵一艘载货6000吨的货轮计划13:30进港卸货,已知该货轮进出港时的水深必须在8m以上,进出港时间忽略不计,且该货轮卸货量p(千吨)与卸货时间x(小时)之间的函数关系如图2所示,该船能在当天离港吗?为什么?
我校部分学生参加了2011年全国初中数学竞赛决赛,并取得优异成绩,已知竞赛成绩都是整数,试题满分为140分,参赛学生的成绩分布情况如下:
根据以上信息解答下列问题:
⑴全市共有多少人参加本次数学竞赛决赛?最低分和最高分在什么范围内?
⑵经竞赛组委会评定,竞赛成绩在60分以上(含60分)的考生均可获得不同等级的奖励,求此次参加本次竞赛决赛考生的获奖比例;
⑶决赛成绩的中位数落在哪个分数段内?
如图,在△ABC中,AD⊥BC,垂足为D,E、F分别是AB、AC的中点.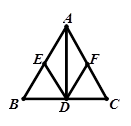
⑴若∠C=70°,求∠AFD的度数
⑵当△ABC满足什么条件时,四边形AEDF为菱形?为什么?
⑶在⑵的基础上,△ABC还需满足什么条件才能使四边形AEDF为正方形?为什么?
某公司每月付给销售人员的工资有两种方案.
方案一:没有底薪,只拿销售提成;
方案二:底薪加销售提成
(注:销售提成是指从销售每件商品得到的销售额中提取一定数量的费用).
设销售商品的数量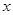 (件),销售人员的月工资
(件),销售人员的月工资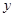 (元).如图所示,
(元).如图所示,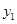 为方案一的函数图象,
为方案一的函数图象, 为方案二的函数图象.从图中信息解答如下问题:
为方案二的函数图象.从图中信息解答如下问题:
⑴求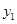 的函数函数关系式;
的函数函数关系式;
⑵求点A的坐标,并说出A点的实际意义;
⑶请问方案二中每月付给销售人员的底薪是多少元?
⑷如果该公司销售人员小丽的月工资要不低于1800元,那么小丽选用哪种方案最好?至少要销售商品多少件?

 中,自变量
中,自变量 的取值范围是 .
的取值范围是 . (
( 为常数)的图像经过点(–1,–2),当x>0时,
为常数)的图像经过点(–1,–2),当x>0时, 随着
随着 的增大而 .(填增大或减小)
的增大而 .(填增大或减小) 的平均数是6,则数据
的平均数是6,则数据 ,
, ,
, 的平均数是 .
的平均数是 .
 中,
中, ,
, 为
为 上一点,AC=5,AB=13,BD =8,
上一点,AC=5,AB=13,BD =8,
 的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C、D都在第一象限.
的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C、D都在第一象限.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号